1. Основы математической статистики
Есть правда, есть большая правда, а есть статистика на Матпрофи.ру!
1.1. Понятие предмета
Математическая статистика следует «вторым эшелоном» за теорией вероятностей, и это не случайность, а логическое продолжение. Отличие состоит в том, что теорвер даёт теоретическую оценку случайным событиям, а статистика работает с практическими или как говорят, эмпирическими данными, которые берутся непосредственно «из жизни».
Что изучает матстат?
Если кратко, то математическая статистика изучает методы сбора и обработки статистической информации для получения научных и практических выводов.
Статистическая – это та, которую можно выразить числами. Эта информация появляется в результате исследования массовых (обычно) явлений, которые носят случайный характер. Она может быть изначально числовой (например, длина чего-либо) или иметь качественную первооснову – «оцифровке» поддаётся даже доброта котиков.
Немедленный пример. Что главное орудие физика? Секундомер:
Пример 1
Студент Константин выполняет лабораторную работу по определению коэффициента вязкости жидкости методом Стокса.
…спокойствие, тут будет всего несколько чисел :)
Экспериментальная часть этой работы состоит в том, что в высокий цилиндрический сосуд с жидкостью сбрасывается достаточно маленький и тяжёлый шарик, после чего замеряется время его погружения.
Время погружения шарика зависит от множества случайных факторов: прямоты рук экспериментатора, погрешности измерения времени, хаотичного движения молекул жидкости и т.д., вплоть до влияния Луны. Поэтому эксперимент целесообразно провести 5-10 раз (как оно обычно и требуется).
Предположим, что в результате 5 опытов получены следующие результаты:
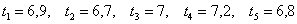 (в секундах) (в секундах)
Что произошло? Студент Костя собрал статистические данные. Они эмпирические (взяты непосредственно из опытов), носят случайный характер (см. выше). И массовый. Ведь все однокурсники только и занимаются тем, что бросают в сосуды шарики, да и мало ли на Земле похожих шариков, которые тонут в похожей жидкости.
Ну а мы потихоньку погружаемся в терминологию:
Полученные экспериментальные значения называются вариантами, а их совокупность – вариационным рядом. Почему так? Потому что полученные значения варьируются под воздействием случайных факторов.
Справка: варианта (существительное женского рода) – в статистике означает отдельно взятое эмпирическое значение.
Далее. Далее Константин должен обработать полученные данные. Во-первых, посмотреть, а нет ли среди них варианты, которая сильно отличается от всех остальных? Наличие такого значения сигнализирует о том, что соответствующий опыт проведён неудачно и его следует исключить из рассмотрения.
Нет, все значения достаточно близкИ друг к другу, и теперь напрашивается вычислить среднюю величину – разделить сумму значений на их 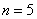 количество: количество:
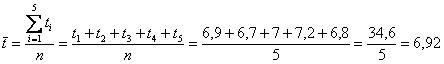 секунды. секунды.
Это значение называют простой средней или, как многие знают, средним арифметическим. Его стандартно обозначают с чёрточкой наверху.
Справка на всякий случай: математический значок 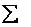 означает суммирование, а переменная означает суммирование, а переменная 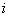 играет роль «счётчика»; в данном случае играет роль «счётчика»; в данном случае 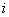 изменяется от 1 до 5. изменяется от 1 до 5.
Если грызут сомнения на счёт точности, то лучше не полениться и провести 10 опытов, что, кстати, удобнее в плане вычислений (на 10 делить проще). И, разумеется, полученный результат будет надёжнее, чем в 1-м случае.
Всё. Статические данные обработаны, осталось сделать выводы. А именно, с помощью значения 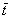 вычислить коэффициент вязкости жидкости и ещё там вроде что-то, желающие могут найти эту лабу в Сети. вычислить коэффициент вязкости жидкости и ещё там вроде что-то, желающие могут найти эту лабу в Сети.
…Возможно, у вас возник вопрос, а почему я выбрал такой пример? Это немногое, что мне запомнилось из институтского курса физики :)
Пример 2
Студенческая группа сдала коллоквиум по матанализу со следующими результатами:
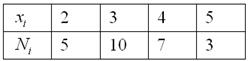
Требуется определить среднюю успеваемость группы
Сбором статистических данных здесь занимался преподаватель, и обратите внимание на их характер: они эмпирические, массовые (громко, конечно, сказано, но таки массовые) и отчасти случайные. Кому-то повезло с вопросом, кому-то нет, кто-то что-то вспомнил / забыл, списал, выпил, прогулял и так далее…, прямо какое-то броуновское движение студентов J
Как нетрудно понять, роль вариант 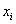 здесь играют полученные оценки, а здесь играют полученные оценки, а 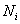 – это соответствующие частоты – количество студентов, которые получили ту или иную оценку. Подсчитаем общую численность группы: – это соответствующие частоты – количество студентов, которые получили ту или иную оценку. Подсчитаем общую численность группы:
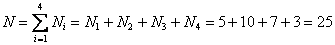 человек и привыкаем к терминам: исследуемое множество называют статистической совокупностью, а его численность – объёмом совокупности. человек и привыкаем к терминам: исследуемое множество называют статистической совокупностью, а его численность – объёмом совокупности.
Теперь обратим внимание на следующую вещь: двоечников и отличников у нас мало, а нормальных студентов :) много. И возникает вопрос: как вычислить «справедливую» среднюю оценку по всей совокупности? Решение напрашивается – с помощью так называемой средневзвешенной средней:
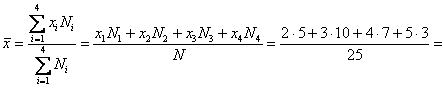
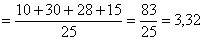 – средняя успеваемость по группе. – средняя успеваемость по группе.
…да, суровые у меня сегодня примеры :) Давайте проанализируем их принципиальные отличия:
1) В первом примере проводится статистическое исследование количественной величины (времени), а во втором «оцифровывается» и анализируется качественный признак (успеваемость).
2) В первой случае исследуемая величина непрерывна, и, строго говоря, все полученные значения различны (отличаются хоть какими-то миллисекундами). Во втором случае варианты дискретны, т.е. представляют собой отдельно взятые изолированные значения. Следует заметить, что они не обязаны быть целыми, так, например, можно ввести в рассмотрение оценки 2,5; 3,5 и 4,5. И у дискретной величины, как правило, есть неоднократно встречающиеся (одинаковые) варианты.
Ставлю важный подзаголовок и продолжаю:
1.2. Генеральная и выборочная совокупность
3) В первом примере речь идёт о выборке значений. Что это значит? Это значит, что шарик можно сбрасывать в воду гораздо бОльшее и теоретически вообще бесконечное количество раз. Таким образом, проведённые 5 опытов – есть, по сути, выборка, которую называют выборочной совокупностью. При этом соответствующее среднее значение принято называть выборочной средней.
Второй пример (с успеваемостью) отличен тем, что в нём исследуется ВСЯ совокупность, и поэтому её называют генеральной совокупностью, а соответствующее среднее значение – генеральной средней. Но такая ситуация редкость. Редко когда удаётся исследовать всю совокупность.
И сейчас мы подошли к краеугольному камню матстата:
1.3. Основной метод математической статистики
Задача
Федор пошёл на базу исследовать помидоры. Требуется определить среднюю массу помидора и среднюю долю первосортных помидоров.
Разбираемся в ситуации. Очевидно, что на базе находится очень и очень много помидоров, обозначим их общее количество через 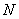 . Это генеральная совокупность объёма . Это генеральная совокупность объёма 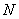 . Для того чтобы решить задачу, можно взвесить каждый овощ: . Для того чтобы решить задачу, можно взвесить каждый овощ: 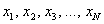 (в граммах, например) и вычислить генеральную среднюю: (в граммах, например) и вычислить генеральную среднюю:
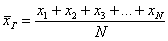 – среднюю массу помидора. – среднюю массу помидора.
Но это долго и трудоёмко, даже если Феде будут помогать все его однокурсники.
Поэтому для оценки параметров генеральной совокупности целесообразно использовать выборочный метод.
Его суть состоит в том, что из генеральной совокупности достаточно выбрать
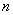 объектов, которые хорошо характеризуют всю совокупность. объектов, которые хорошо характеризуют всю совокупность.
Это «хорошо» называют представительностью или, как говорят буржуи, репрезентативностью выборки.
Проговорим сиё модное слово вслух: ре-пре-зен-та-тив-ность.
…Молодцы! А то некоторым студентам из года в год слышится «презервативы» J Радует, однако, что это не плохое слово :)
Что нужно для того, чтобы обеспечить репрезентативность?
Во-первых, выборка должна быть достаточно велика, помидоров так 500-1000 точно, что уже вполне по силам даже одному Феде.
Замечание: в дальнейшем мы сформулируем более строгие статистические критерии на счёт оптимального объёма выборки.
Во-вторых, отбор следует осуществлять равномерно – из каждого ящика.
В-третьих, отбор должен быть случайным. Для этого используются разные приёмы, самый простой из них – выбор «вслепую» из случайно выбранного места ящика, обязательно с разной глубины (а то мало ли что поставщик мог там спрятать).
…Да-да! Я буду обучать вас реальной статистике :)
И, в-четвёртых (а может быть, и, в-первых), есть и другие факторы. В частности, важно знать, а однородна ли генеральная совокупность? Так, если помидоры поступили от разных поставщиков, то каждую партию полезно исследовать по отдельности (сделать несколько независимых выборок).
Итак, пусть Фёдор по всем правилам выбрал 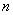 помидоров, и теперь дело за малым – взвесить каждый овощ: помидоров, и теперь дело за малым – взвесить каждый овощ: 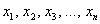 (граммы) и вычислить выборочную среднюю: (граммы) и вычислить выборочную среднюю:
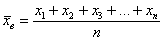 – среднюю массу помидора в выборке. – среднюю массу помидора в выборке.
При этом очевидно, что чем больше объем 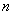 выборочной совокупности, тем полученное значение выборочной совокупности, тем полученное значение 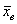 будет точнее приближать генеральную среднюю будет точнее приближать генеральную среднюю 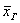 . .
Но фишка состоит в том, что если начать увеличивать выборку в два, три и бОльшее количество раз, то будут получаться выборочные средние, которые мало отличаются от уже рассчитанного значения 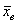 . Вы спрОсите, как это установлено? Эмпирически, в результате огромного количества проведённых исследований. А затем данный факт был подтверждён и теоретически. . Вы спрОсите, как это установлено? Эмпирически, в результате огромного количества проведённых исследований. А затем данный факт был подтверждён и теоретически.
Таким образом, нет никакого практического смысла тратить силы, время, нервы и деньги на исследование бОльшей выборки и тем более, всей генеральной совокупности.
Вот оно как – в статистике есть и прямая экономическая выгода!
И технический момент, обратите внимание на используемые буквы – они стандартны. Вместо «иксов» иногда используют «игреки», а вместо «эн» – 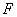 и и 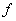 . Иные буквы применяйте, только если их любит ваш преподаватель или они в вашей методичке. . Иные буквы применяйте, только если их любит ваш преподаватель или они в вашей методичке.
Вторая часть задачи. Оценим вместе с Федей долю первосортных помидоров на базе. Для этого, разумеется, не нужно заново «шерстить» всю генеральную совокупность, анализируется та же самая выборка.
В отличие от первого пункта, здесь исследуется уже качественный признак, для которого, тем не менее, можно сформулировать чёткие критерии. Пусть первосортный помидор – это чёрный, лысый красный, спелый, без видимых дефектов, массой выше среднего. Совершенно понятно, что генеральная совокупность содержит 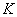 таких помидоров, и существует точное значение: таких помидоров, и существует точное значение:
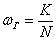 – генеральная доля первосортных помидоров. – генеральная доля первосортных помидоров.
Однако по причине трудозатрат и нецелесообразности полного исследования, достаточно подсчитать количество 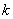 таких овощей в выборке и вычислить: таких овощей в выборке и вычислить:
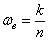 – выборочную долю, которая будет близкА к истинному значению – выборочную долю, которая будет близкА к истинному значению 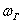 . Но это только, напомню, при условии грамотно организованной и проведённой выборки. . Но это только, напомню, при условии грамотно организованной и проведённой выборки.
Доля, как вы догадываетесь, может принимать значения от 0 до 1, и нередко её домножают на 100, чтобы выразить этот показатель в процентах.
Готово.
Константин, Фёдор, спасибо за участие, а остальные, как в том анекдоте, поедут «на картошку» :) В качестве разминки предлагаю вам задачу с тремя пунктами различного уровня сложности:
Пример 3
а) Урожайность картофеля по трём областям за ** год составила 147, 145, 155 ц/га. Требуется вычислить среднюю урожайность.
Метрическая справка: 1 центнер = 100 кг, 1 тонна = 1000 кг;
1 гектар (га) = 10000 квадратных метров;
показатель ц/га означает, сколько центнеров собрано в среднем с 1 гектара.
Вариация чуть сложнее:
б) Известны следующие данные по трём областям:

…Вы думаете, тут исследована вся генеральная совокупность? Нет, эти циферки нарисовали чиновники для отчёта! – привыкайте к настоящей статистике:)))
Требуется вычислить среднюю урожайность.
И третий пункт, творческий:
в) Вычислить среднюю урожайность по следующим данным:

«Валовой» – это значит, всего собрано по области.
ДУМАЕМ, ВНИКАЕМ и РАССУЖДАЕМ – принцип здесь точно такой же, как и при решении задач по теории вероятностей. И не забываем приписывать к результатам размерность! (секунды, граммы и т.д., а в данном случае – ц/га). За сию небрежность вас накажут не только на физике ;)
Решения с пояснениями в конце книги.
В заключение вводной главы систематизируем самое важное:
Математическая статистика – это наука, изучающая методы сбора и обработки статистической информации для получения научных и практических выводов.
Основным методом математической статистики является выборочный метод, его суть состоит в исследовании представительной выборочной совокупности – для достоверной оценки совокупности генеральной. Данный метод экономит временнЫе, трудовые и материальные затраты, поскольку исследование всей совокупности зачастую затруднено либо невозможно.
Иногда матстат считают разделом математики. И это тоже правда! :) Желаю успехов в дальнейшем освоении курса! Вперёд без страха и сомнений:
 2. Вариационные ряды 2. Вариационные ряды
| Оглавление |
|