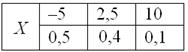
2.2.3. Дисперсия дискретной случайной величины

В предыдущем параграфе мы выяснили, насколько полезно знать математическое ожидание, однако только этой характеристики ещё не достаточно для описания случайной величины. Представим двух стрелков, которые стреляют по мишени. Один стреляет метко и попадает близко к центру, а другой… просто развлекается и даже не целится. Но что забавно, их средние результаты будет одинаковыми! Эту ситуацию условно иллюстрируют следующие случайные величины:

«Снайперское» математическое ожидание равно , однако и у «интересной личности» оно тоже нулевое!

Таким образом, возникает надобность количественно оценить, насколько далеко рассеяны пули (значения случайной величины) относительно центра мишени (математического ожидания). Ну а рассеяние с латыни переводится не иначе, как дисперсия.

Посмотрим, как определяется эта числовая характеристика на одном из предыдущих примеров:

Мы уже нашли неутешительное математическое ожидание этой игры, и сейчас нам предстоит вычислить её дисперсию, которая обозначается через .

Выясним, насколько далеко «разбросаны» выигрыши / проигрыши относительно среднего значения. Очевидно, что для этого нужно вычислить разности между значениями случайной величины и её математическим ожиданием:

–5 – (–0,5) = –4,5
2,5 – (–0,5) = 3
10 – (–0,5) = 10,5

Теперь вроде бы нужно просуммировать результаты, но этот путь не годится – по той причине, что отрицательные и положительные отклонения будут взаимоуничтожаться

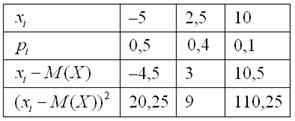
Чтобы обойти эту неприятность можно рассмотреть модули разностей, но по техническим причинам прижился подход, когда их возводят в квадрат. Решение удобно оформлять таблицей:

И здесь напрашивается вычислить среднеожидаемое значение квадратов отклонений. А это ЧТО за значение? Это их математическое ожидание, которое и является мерилом рассеяния, проговариваем и ОСМЫСЛИВАЕМ это определение:

– Дисперсия – это математическое ожидание квадратов отклонений случайной величины от её математического ожидания.

и из определения сразу следует, что дисперсия не может быть отрицательной – возьмите этот факт на заметку!

Теперь вспоминаем, как находить матожидание. Для этого нужно перемножить «пациентов» на соответствующие вероятности (продолжение таблицы):

и просуммировать результаты:

…Но не кажется ли вам, что на фоне выигрышей результат получился великоватым? Всё верно – мы возводили в квадрат, и чтобы вернуться в размерность нашей игры, нужно извлечь квадратный корень. Данная величина называется:

2.2.4. Среднее квадратическое отклонение

2.2.2. Математическое ожидание дискретной случайной величины

| Оглавление |

Полную и свежую версию этой книги в pdf-формате,
а также курсы по другим темам можно найти после Оглавления.

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!

С наилучшими пожеланиями, Александр Емелин