|
Ваш репетитор, справочник и друг!
|
4.5.2. Правило треугольниковАналогично определителю «два на два», определитель «три на три» можно вычислить с помощью специальной формулы: …Есть ли какая-то закономерность в формуле? Конечно. Если вы посмОтрите на любую тройку множителей, то заметите, что все элементы в ней
расположены в разных строках и разных столбцах. Причём, элементы Зеркально с отрицательными слагаемыми формулы: члены Отсюда и название: формула (правило) треугольников. Пример 56 Вычислить определитель матрицы ВНИМАТЕЛЬНО используем соответствующую формулу: Готово. Формула треугольников хоть и понятная, но длинная и допустить ошибку по невнимательности проще простого. Как избежать досадных промахов? Здесь можно воспользоваться тем же Матричным калькулятором (приложен к книге), но если вы допустите ошибку, то всё равно замучаетесь её искать. В этой связи целесообразно применить второй способ вычисления определителя, который фактически совпадает с первым: |
|
© mathprofi.ru - mathter.pro, 2010-2025, сделано в Блокноте. |

 Высшая алгебра для начинающих
Высшая алгебра для начинающих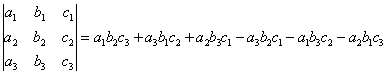
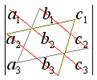
 по правилу
треугольников
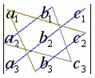
по правилу
треугольников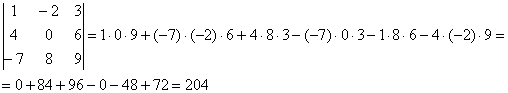
 4.5.3. Формула Саррюса
4.5.3. Формула Саррюса 4.5.1. Определитель матрицы
4.5.1. Определитель матрицы