1.5.2. Как найти длину отрезка?

Длина, как уже отмечалось, обозначается знаком модуля.

Если даны две точки плоскости и , то длину отрезка можно вычислить по формуле:

Если даны две точки пространства и , то длину отрезка можно вычислить по формуле:

Примечание: соответствующие координаты можно переставить местами: и , но это нестандартный вариант.

Задача 3

Даны точки и . Найти длину отрезка .

Решение: по соответствующей формуле:

Ответ: (единицы)

Обратите внимание на вынесение множителя из-под корня: (см. Приложение Школьные материалы). Это крайне желательное действие, если оно возможно. Ибо будет придирка со стороны преподавателя. С высокой вероятностью.

И для наглядности снова выполню чертёж, тут есть что сказать:

Отрезок – это не вектор, а обычный ненаправленный отрезок. И перемещать его куда-либо, конечно, нельзя.

Кроме того, если вы выполните чертеж в масштабе: 1 ед. = 1 см (две тетрадные клетки), то полученный ответ можно проверить обычной линейкой, непосредственно измерив длину отрезка . Но проще, конечно, использовать Калькулятор (приложен к книге).

Кстати, в ответе не забываем указать размерность: «единицы». В условии не сказано, ЧТО это – миллиметры, сантиметры, метры или километры. Поэтому математически грамотным решением будет общая формулировка: «единицы» – сокращенно «ед.».

Задание для самостоятельного решения с отрезком в пространстве:

Задача 4

Даны точки и . Найти длину отрезка .

Решение и ответ в конце книги.

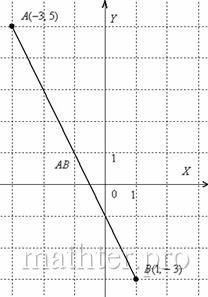
1.5.3. Как найти длину вектора?

1.5.1. Как найти вектор по двум точкам?

| Оглавление |

Автор: Aлeксaндр Eмeлин