|
Ваш репетитор, справочник и друг!
|
1.5.3. Как найти длину вектора?Если дан вектор плоскости Задача 5 Даны точки Я взял те же точки, что и в Задаче 3. Решение: сначала найдём вектор Ответ: Приближенные значения, в принципе, можно и не указывать, но я рекомендую. Округляют обычно до 1-2, иногда до 3-4 знаков после запятой А теперь ответим на вопрос: в чём здесь принципиальное отличие от Задачи 3?
А в чём сходство этих задач? Очевидно, что длина простого отрезка Задачу 3 можно было решить и другим способом, а именно вместо применения формулы Этот способ широко практикуется в ходе решений задач аналитической геометрии. Вышесказанное справедливо и для пространственного случая Тренируемся самостоятельно: Задача 6 а) Даны точки Решения и ответы в конце книги.
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников»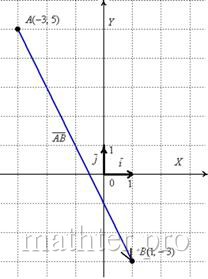 Отличие состоит в том, что
здесь речь идёт о векторе, а не об обычном отрезке. Вектор можно переместить в любую точку плоскости, переобозначив его,
например, буквой
Отличие состоит в том, что
здесь речь идёт о векторе, а не об обычном отрезке. Вектор можно переместить в любую точку плоскости, переобозначив его,
например, буквой  1.5.4. Действия с векторами в координатах
1.5.4. Действия с векторами в координатах 1.5.2. Как найти длину отрезка?
1.5.2. Как найти длину отрезка?