|
Ваш репетитор, справочник и друг!
|
1.5.4. Действия с векторами в координатахРанее мы рассмотрели правила сложения векторов и умножения вектора на число. Но рассмотрели их с принципиально-графической точки
зрения. Посмотрим, как данные правила работают аналитически – когда нам известны координаты векторов в ортонормированном
базисе 1) Правило сложения векторов. Пусть есть два вектора плоскости 2) Правило умножения вектора на число. Ещё проще! Для того чтобы вектор Задача 7 Даны векторы Решение чисто аналитическое: Ответ: Чертеж в подобных задачах строить не надо, тем не менее, геометрическая демонстрация будет весьма полезной. Если считать,
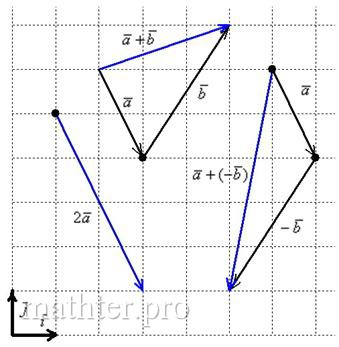
что векторы заданы в ортонормированном базисе Коль скоро речь идет только о векторах, то оси рисовать не обязательно. Достаточно начертить базисные векторы, причём, где угодно. Ну и координатную сетку для удобства. Как видите, графический способ решения привёл к тем же результатам, что и аналитический способ решения. Ещё раз заметьте свободу векторов: любую из трёх «конструкций» можно переместить в любую точку плоскости. Для векторов в пространстве можно провести аналогичные выкладки. Но там чертежи строить значительно сложнее, поэтому ограничусь аналитическим решением (на практике, собственно, бОльшего и не нужно): Задача 8 Даны векторы Решение: для действий с векторами справедлив обычный алгебраический приоритет: сначала умножаем, потом складываем: Ответ: И для самостоятельного решения занятный пример с векторами на плоскости: Задача 9 Даны векторы Решение и ответ в конце книги.
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников»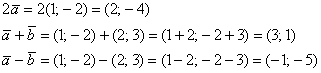
 1.5.5. Как найти единичный вектор?
1.5.5. Как найти единичный вектор? 1.5.3. Как найти длину вектора?
1.5.3. Как найти длину вектора?