1.3. Основные действия с векторами
В школьном курсе геометрии рассматривается ряд действий и правил с векторами, и для начала мы повторим наиболее важные из
них:
Правило сложения векторов по правилу треугольников
Рассмотрим два произвольных ненулевых вектора 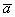 и и 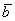 : :
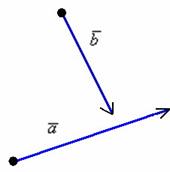
Требуется найти их сумму. В силу того, что все векторы свободны, отложим
вектор 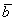 от конца вектора от конца вектора 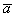 : :
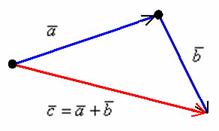
Суммой векторов 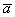 и и 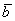 является вектор является вектор 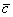 . Для лучшего понимания правила в него целесообразно вложить физический смысл: пусть
некоторое тело совершило путь по вектору . Для лучшего понимания правила в него целесообразно вложить физический смысл: пусть
некоторое тело совершило путь по вектору 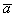 , а
затем по вектору , а
затем по вектору 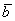 . Тогда сумма векторов . Тогда сумма векторов 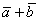 представляет собой вектор результирующего пути представляет собой вектор результирующего пути 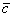 с началом в точке отправления и концом в точке
прибытия. с началом в точке отправления и концом в точке
прибытия.
Векторы перестановочны: 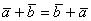 – мысленно отложите
вектор – мысленно отложите
вектор 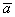 от конца вектора от конца вектора 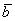 (см. рисунок выше), и вы поймёте, что получится тот же самый
вектор (см. рисунок выше), и вы поймёте, что получится тот же самый
вектор 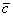 . .
Аналогичное правило справедливо для суммы любого количества векторов. Как говорится, тело может пройти свой путь по
зигзагу, а может и на автопилоте по результирующему вектору суммы.
Кстати, если вектор 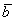 отложить от начала вектора отложить от начала вектора 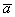 , то получится эквивалентное правило параллелограмма сложения векторов. , то получится эквивалентное правило параллелограмма сложения векторов.
Умножение вектора на число
Произведением ненулевого вектора 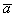 на число на число 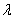 является такой вектор является такой вектор 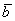 , длина которого равна , длина которого равна 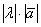 , причём при , причём при 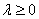 векторы векторы 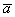 и и 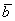 сонаправлены, а при сонаправлены, а при 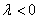 направлены противоположно. направлены противоположно.
Правило умножения вектора на число легче понять с помощью рисунка:
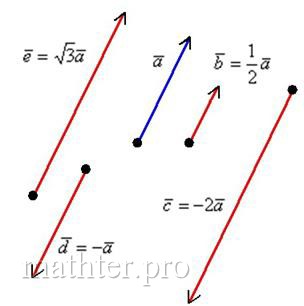
Разбираемся более детально:
1) Направление. Если множитель 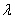 отрицательный, то полученный вектор будет направлен в противоположную сторону –
смотрим на векторы отрицательный, то полученный вектор будет направлен в противоположную сторону –
смотрим на векторы 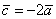 и и 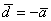 . .
2) Длина. Если множитель заключен в пределах 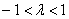 , то длина вектора соразмерно уменьшается. Так, длина вектора , то длина вектора соразмерно уменьшается. Так, длина вектора 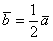 в два раза меньше длины вектора в два раза меньше длины вектора 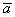 . Если множитель . Если множитель 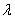 по модулю больше единицы, то длина вектора увеличивается в по модулю больше единицы, то длина вектора увеличивается в 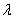 раз. Так, длина вектора раз. Так, длина вектора 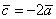 в два раза больше длины вектора в два раза больше длины вектора 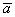 . .
3) Очевидно, что все векторы коллинеарны, при этом
один вектор линейно* выражен через другой, например, 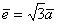 . Обратное тоже справедливо: если один вектор можно линейно выразить через другой, то такие векторы обязательно коллинеарны. Таким образом: если мы умножаем вектор на число, то
получится коллинеарный (по отношению к исходному) вектор. . Обратное тоже справедливо: если один вектор можно линейно выразить через другой, то такие векторы обязательно коллинеарны. Таким образом: если мы умножаем вектор на число, то
получится коллинеарный (по отношению к исходному) вектор.
* Справка: линейно – это значит, через множитель-константу.
4) Векторы  сонаправлены. Векторы сонаправлены. Векторы 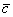 и и 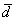 тоже
сонаправлены. Любой вектор первой группы противоположно направлен по отношению к любому вектору второй группы. тоже
сонаправлены. Любой вектор первой группы противоположно направлен по отношению к любому вектору второй группы.
 1.4. Координаты вектора на плоскости и в пространстве 1.4. Координаты вектора на плоскости и в пространстве
 1.2. Коллинеарность векторов 1.2. Коллинеарность векторов
| Оглавление |
|

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников»


 1.4. Координаты вектора на плоскости и в пространстве
1.4. Координаты вектора на плоскости и в пространстве 1.2. Коллинеарность векторов
1.2. Коллинеарность векторов