1.4. Координаты вектора на плоскости и в пространстве
Сначала рассмотрим векторы на плоскости. Изобразим декартову прямоугольную систему координат и от начала координат
отложим единичные векторы 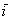 и и 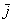 . Опять знакомая школьная картинка: . Опять знакомая школьная картинка:
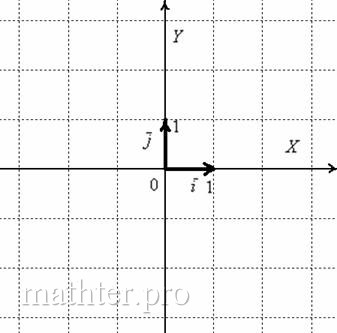
Векторы 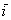 и и 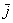 ортогональны. А вот здесь можно также сказать, что векторы перпендикулярны. Но лучше ортогональны. Привыкаем к новым терминам! ортогональны. А вот здесь можно также сказать, что векторы перпендикулярны. Но лучше ортогональны. Привыкаем к новым терминам!
Обозначение: ортогональность векторов записывают привычным значком перпендикулярности, например: 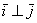 . .
Рассматриваемые векторы называют координатными векторами или ортами. Данные векторы образуют базис на плоскости.
Определение базиса мы сформулируем позже, а пока на уровне понимания: векторы базиса задают «координатную сетку». Да-да,
прямо эту клетчатую разлиновку, которую вы видите на чертеже выше.
Иногда построенный базис называют ортонормированным базисом плоскости, «орто» – потому что координатные векторы
ортогональны. Прилагательное «нормированный» в переводе с математического на русский означает единичный, т.е. длины
векторов этого базиса равны единице.
Обозначение: базис обычно записывают в круглых скобках, внутри которых в строгой последовательности перечисляются базисные векторы, например: 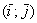 .
Координатные векторы переставлять местами нельзя. .
Координатные векторы переставлять местами нельзя.
Любой вектор 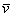 плоскости единственным образом выражается в виде: плоскости единственным образом выражается в виде:
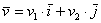 , где , где 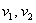 – числа, которые называются координатами вектора в данном базисе. Само
выражение – числа, которые называются координатами вектора в данном базисе. Само
выражение 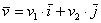 называют разложением вектора называют разложением вектора 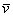 по базису по базису  . .
И примеры, примеры, примеры:
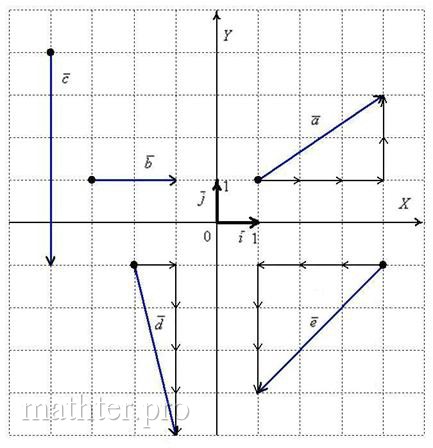
Начнём с вектора 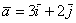 . По чертежу хорошо видно, что
при разложении вектора по базису используются только что рассмотренные: . По чертежу хорошо видно, что
при разложении вектора по базису используются только что рассмотренные:
1) правило умножения вектора на число: 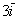 и и 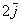 ; ;
2) сложение векторов по правилу треугольника: 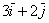 . .
А теперь мысленно отложите вектор 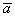 от любой
другой точки плоскости. Совершенно понятно, что его разложение от любой
другой точки плоскости. Совершенно понятно, что его разложение 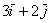 будет «неотступно следовать за ним». Вот она, свобода вектора! Это свойство, разумеется, справедливо для любого вектора.
Забавно, что сами базисные (свободные) векторы будет «неотступно следовать за ним». Вот она, свобода вектора! Это свойство, разумеется, справедливо для любого вектора.
Забавно, что сами базисные (свободные) векторы 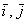 можно начертить где угодно. Правда, делать так не нужно, а то преподаватель тоже
проявит оригинальность и нарисует вам «зачтено» в неожиданном месте :) можно начертить где угодно. Правда, делать так не нужно, а то преподаватель тоже
проявит оригинальность и нарисует вам «зачтено» в неожиданном месте :)
Векторы 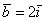 , , 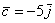 иллюстрируют правило умножения вектора на
число, вектор иллюстрируют правило умножения вектора на
число, вектор 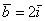 сонаправлен с базисным вектором сонаправлен с базисным вектором 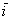 , вектор , вектор 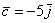 направлен противоположно по отношению к
базисному вектору направлен противоположно по отношению к
базисному вектору 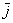 . У этих векторов одна из
координат равна нулю, дотошно можно записать так: . У этих векторов одна из
координат равна нулю, дотошно можно записать так: 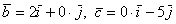 . .
И, наконец: 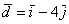 , , 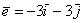 . Кстати, что такое вычитание векторов, и почему я не напомнил вам о
правиле вычитания? А потому что не нужно. С алгебраической точки зрения, вычитание – это частный случай сложения.
Так, разложения векторов «дэ» и «е» преспокойно записываются в виде суммы: . Кстати, что такое вычитание векторов, и почему я не напомнил вам о
правиле вычитания? А потому что не нужно. С алгебраической точки зрения, вычитание – это частный случай сложения.
Так, разложения векторов «дэ» и «е» преспокойно записываются в виде суммы: 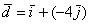 , , 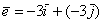 . Проследите по чертежу, как чётко в этих ситуациях работает старое доброе сложение векторов по правилу треугольника . Проследите по чертежу, как чётко в этих ситуациях работает старое доброе сложение векторов по правилу треугольника
Разложение вида 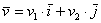 иногда называют
разложением вектора в системе орт (т.е. в системе единичных векторов). Но это не единственный способ записи вектора,
на практике распространён следующий вариант: иногда называют
разложением вектора в системе орт (т.е. в системе единичных векторов). Но это не единственный способ записи вектора,
на практике распространён следующий вариант:
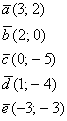 или (реже) со знаком равенства: или (реже) со знаком равенства: 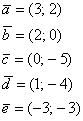
то есть, в круглых скобках в строгой последовательности указываются координаты вектора. В практических
задачах используются все три варианта записи.
Сами базисные векторы можно записать так: 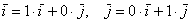 или,
соответственно: или,
соответственно: 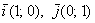 . .
С координатами на плоскости разобрались. Теперь рассмотрим векторы в трехмерном пространстве, здесь практически всё так
же! Только добавится ещё одна координата. Трехмерные чертежи выполнять тяжко, поэтому ограничусь одним вектором, который для
простоты отложу от начала координат:
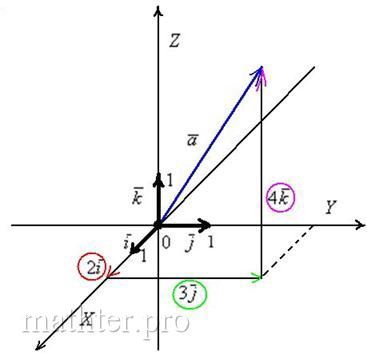
Перед вами ортонормированный базис 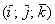 трёхмерного пространства, единичные векторы трёхмерного пространства, единичные векторы 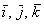 данного базиса попарно ортогональны: данного базиса попарно ортогональны: 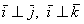 и и 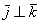 . Ось . Ось 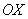 наклонена под углом 45 градусов для того, чтобы
складывалось визуальное впечатление пространства. наклонена под углом 45 градусов для того, чтобы
складывалось визуальное впечатление пространства.
Любой вектор 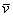 трехмерного
пространства можно единственным способом разложить по ортонормированному базису трехмерного
пространства можно единственным способом разложить по ортонормированному базису 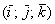 : :
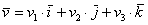 , где , где 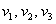 – координаты вектора – координаты вектора 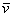 (числа) в этом базисе. (числа) в этом базисе.
Пример с картинки: 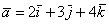 . Давайте посмотрим, как
здесь работают правила действий с векторами. Во-первых, умножение вектора на
число: . Давайте посмотрим, как
здесь работают правила действий с векторами. Во-первых, умножение вектора на
число: 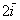 (красная стрелка), (красная стрелка), 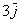 (зеленая стрелка) и (зеленая стрелка) и 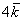 (малиновая стрелка). Во-вторых, перед вами пример сложения нескольких, в данном случае трёх векторов: (малиновая стрелка). Во-вторых, перед вами пример сложения нескольких, в данном случае трёх векторов: 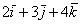 . Вектор суммы . Вектор суммы 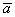 начинается в исходной точке отправления (начало вектора начинается в исходной точке отправления (начало вектора 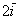 ) и утыкается в итоговую точку прибытия (конец вектора ) и утыкается в итоговую точку прибытия (конец вектора 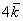 ). ).
Все векторы трехмерного пространства, естественно, тоже свободны,
попробуйте мысленно отложить вектор 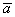 от любой
другой точки, и вы поймёте, что его разложение от любой
другой точки, и вы поймёте, что его разложение 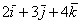 «останется при нём». «останется при нём».
Аналогично «плоскому» случаю, помимо записи 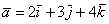 , широко используются версии со скобками: , широко используются версии со скобками: 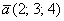 либо либо 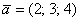 . .
Если в разложении отсутствует один (или два) координатных вектора, то вместо них ставятся нули. Примеры:
вектор 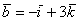 (дотошно (дотошно 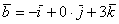 ) – запишем ) – запишем 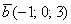 ; ;
вектор 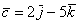 (дотошно (дотошно 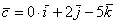 ) – запишем ) – запишем 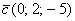 ; ;
вектор 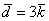 (дотошно (дотошно 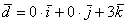 ) – запишем ) – запишем 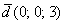 . .
Базисные векторы записываются следующим образом:
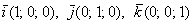
И мы переходим к практике, которая нас уже заждалась.
Рассмотренные ниже задания крайне желательно научиться решать «на полном автомате», а формулы запомнить
наизусть, ...впрочем, запоминать не надо – сами запомнятся :) Изложение материала пойдет «параллельным курсом» – и
для плоскости, и для пространства. По той причине, что формулы однотипны:
 1.5.1. Как найти вектор по двум точкам? 1.5.1. Как найти вектор по двум точкам?
 1.3. Основные действия с векторами 1.3. Основные действия с векторами
| Оглавление |
|

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников»

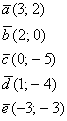 или (реже) со знаком равенства:
или (реже) со знаком равенства: 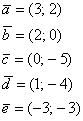

 1.5.1. Как найти вектор по двум точкам?
1.5.1. Как найти вектор по двум точкам? 1.3. Основные действия с векторами
1.3. Основные действия с векторами