1.5.5. Как найти единичный вектор?
Единичный вектор – это вектор, длина которого в ортонормированном базисе равна единице. Таковыми являются сами
координатные векторы 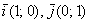 и и 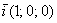 , , 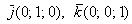 и противоположно направленные им векторы, например: и противоположно направленные им векторы, например:
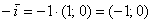
То, что их длина равна единице, элементарно видно не только по чертежам, но и по формулам 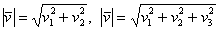 . .
А теперь рассмотрим произвольный вектор 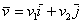 либо либо
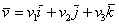 и поставим задачу найти
единичный вектор и поставим задачу найти
единичный вектор 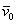 , коллинеарный исходному. Таких векторов будет два. Чтобы найти сонаправленный единичный вектор нужно каждую координату вектора , коллинеарный исходному. Таких векторов будет два. Чтобы найти сонаправленный единичный вектор нужно каждую координату вектора 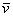 разделить на его длину: разделить на его длину:
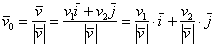 либо либо 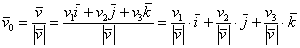 , ,
или, что то же самое – умножить каждую координату вектора 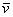 на на 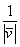 . То
есть, деление – это частный случай умножения (осознаём и привыкаем). Противоположно направленный единичный
вектор очевиден: . То
есть, деление – это частный случай умножения (осознаём и привыкаем). Противоположно направленный единичный
вектор очевиден:
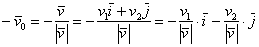 либо либо 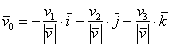
Задача 10
Найти единичные векторы, коллинеарные векторам а) 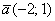 , б) , б) 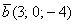 . Выполнить проверку. . Выполнить проверку.
Решение: а) вычислим длину вектора 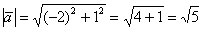 и найдём
сонаправленный единичный вектор: и найдём
сонаправленный единичный вектор:
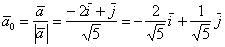 , от иррациональности в знаменателе (корня) тут
обычно не избавляются. Проверка состоит в нахождении длины полученного вектора: , от иррациональности в знаменателе (корня) тут
обычно не избавляются. Проверка состоит в нахождении длины полученного вектора:
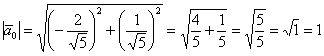 , что и требовалось проверить. , что и требовалось проверить.
Второй вектор очевиден: 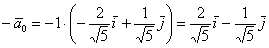 , как очевидна и его
длина , как очевидна и его
длина 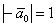 . .
Ответ: 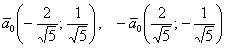
Потребность найти единичный вектор возникает не только в геометрических задачах, и поэтому обязательно прорешайте пункт б)
самостоятельно.
 1.5.6. Деление отрезка в данном отношении 1.5.6. Деление отрезка в данном отношении
 1.5.4. Действия с векторами в координатах 1.5.4. Действия с векторами в координатах
| Оглавление |
|

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников»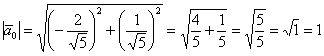 , что и требовалось проверить.
, что и требовалось проверить. 1.5.6. Деление отрезка в данном отношении
1.5.6. Деление отрезка в данном отношении 1.5.4. Действия с векторами в координатах
1.5.4. Действия с векторами в координатах