1.5.6. Деление отрезка в данном отношении
Рассмотрим пару точек 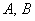 (плоскости или
пространства) и отрезок (плоскости или
пространства) и отрезок 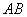 : :

Что будем с ним делать? На это раз пилить. Точкой 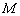 : :

В данном примере точка 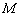 делит отрезок делит отрезок 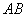 ТАКИМ образом, что отрезок ТАКИМ образом, что отрезок 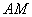 в два раза короче отрезка в два раза короче отрезка 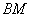 . ЕЩЁ можно сказать, что точка . ЕЩЁ можно сказать, что точка 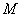 делит отрезок делит отрезок 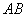 в отношении в отношении 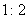 («один к двум»), считая от вершины («один к двум»), считая от вершины  . .
На сухом математическом языке этот факт записывают пропорцией 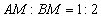 или чаще в виде привычной дроби: или чаще в виде привычной дроби: 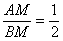 . Отношение отрезков принято стандартно обозначать греческой буквой «лямбда», в данном
случае: . Отношение отрезков принято стандартно обозначать греческой буквой «лямбда», в данном
случае: 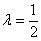 . .
Пропорцию можно составить и в другом порядке: 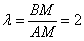 –
сия запись означает, что отрезок –
сия запись означает, что отрезок 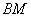 в два раза
длиннее отрезка в два раза
длиннее отрезка 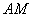 , но какого-то принципиального
значения для решения задач это не имеет. Можно так, а можно так. , но какого-то принципиального
значения для решения задач это не имеет. Можно так, а можно так.
Разумеется, отрезок легко разделить в каком-нибудь другом отношении, и в качестве закрепления понятия второй пример:

Здесь справедливо соотношение: 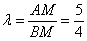 . Если составить
пропорцию наоборот, тогда получаем: . Если составить
пропорцию наоборот, тогда получаем: 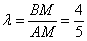 . .
Формулы деления отрезка в данном отношении:
Если известны две точки плоскости 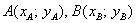 , то
координаты точки , то
координаты точки 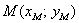 , которая делит отрезок , которая делит отрезок 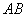 в отношении в отношении 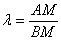 , выражаются формулами: , выражаются формулами:
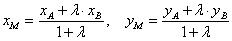
В пространственном случае 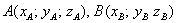 и и 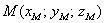 добавляется дополнительная координата: добавляется дополнительная координата:
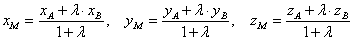 . .
Откуда взялись данные формулы? В курсе аналитической геометрии эти формулы выводятся с помощью векторов (куда ж теперь
без них? =)).
Задача 11
Найти координаты точки 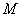 , делящей отрезок , делящей отрезок 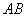 в отношении в отношении 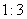 , если известны точки , если известны точки 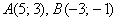
Решение: по умолчанию, отсчёт начинается от первого конца отрезка: 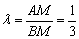 . По формулам деления отрезка в данном отношении, найдём точку . По формулам деления отрезка в данном отношении, найдём точку 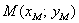 : :
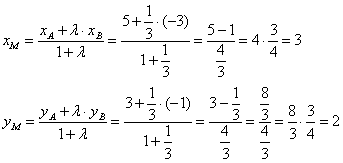
Ответ: 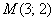
Обратите внимание на технику вычислений: сначала нужно отдельно вычислить числитель и отдельно знаменатель. В результате
чего часто (но далеко не всегда) получается трёх- или четырёхэтажная дробь. После этого избавляемся от
многоэтажности дроби (см. Приложение Школьные материалы) и проводим окончательные
упрощения.
В задаче не требуется строить чертежа, но его полезно выполнить на черновике:
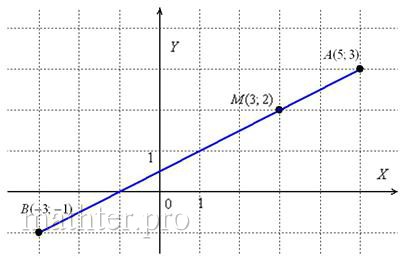
– чтобы убедиться в том, что соотношение 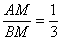 действительно выполнено, то есть отрезок действительно выполнено, то есть отрезок 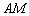 в три раза короче отрезка в три раза короче отрезка 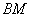 . Если длины не очевидны, то отрезки всегда можно тупо измерить обычной
линейкой. . Если длины не очевидны, то отрезки всегда можно тупо измерить обычной
линейкой.
Существует и второй способ решения: в нём отсчёт начинается с точки 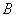 и справедливым является отношение: и справедливым является отношение: 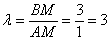 (иными словами, отрезок (иными словами, отрезок 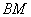 в три раза длиннее отрезка в три раза длиннее отрезка 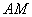 ). По формулам деления отрезка в данном отношении: ). По формулам деления отрезка в данном отношении:
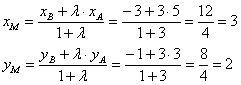
Ответ: 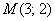
Заметьте, что в формулах необходимо переместить координаты точки 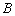 на первое место, поскольку маленький триллер начинался именно с неё. Также видно, что
второй способ рациональнее ввиду более простых вычислений. Но всё-таки данную задачу чаще решают в «традиционном» порядке.
Так, если по условию дан отрезок на первое место, поскольку маленький триллер начинался именно с неё. Также видно, что
второй способ рациональнее ввиду более простых вычислений. Но всё-таки данную задачу чаще решают в «традиционном» порядке.
Так, если по условию дан отрезок 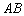 , то
предполагается, что вы составите пропорцию , то
предполагается, что вы составите пропорцию 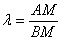 ,
если дан отрезок ,
если дан отрезок 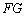 , то «негласно» подразумевается
пропорция , то «негласно» подразумевается
пропорция 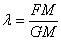 , и так далее. , и так далее.
Задача 12
а) Точка 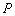 принадлежит отрезку принадлежит отрезку 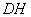 . Известно, что отрезок . Известно, что отрезок 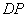 в два раза длиннее отрезка в два раза длиннее отрезка 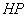 . Найти точку . Найти точку 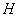 ,
если ,
если 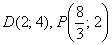 . Выполнить проверку. . Выполнить проверку.
б) Даны точки 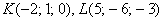 . Найти точку . Найти точку 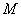 , делящую отрезок , делящую отрезок 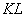 в отношении в отношении 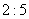 . .
Удачного распила!
 1.5.7. Формулы координат середины отрезка 1.5.7. Формулы координат середины отрезка
 1.5.5. Как найти единичный вектор? 1.5.5. Как найти единичный вектор?
| Оглавление |
|

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников»

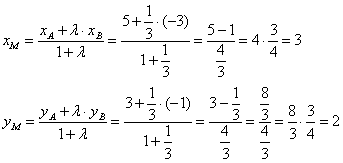

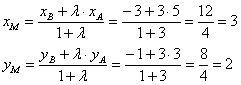
 1.5.7. Формулы координат середины отрезка
1.5.7. Формулы координат середины отрезка 1.5.5. Как найти единичный вектор?
1.5.5. Как найти единичный вектор?