|
Ваш репетитор, справочник и друг!
|
4.3. Взаимосвязь прямоугольной и полярной системы координатОчевидным образом присоединим к полярной системе прямоугольную систему координат Полученные формулы открывают ещё одну лазейку в задаче построения, когда можно обойтись вообще без транспортира: сначала находим декартовы координаты точки (понятно, на черновике), затем мысленно находим нужное место на чертеже и отмечаем данную точку. Затем проводим тонкую прямую, которая проходит через построенную точку и полюс. В результате получается, что угол якобы был отмерян транспортиром. Совсем отчаянные студенты могут обойтись даже без линейки, используя вместо неё ровный край учебника, тетради или зачётной книжки – ведь о метрике позаботились производители тетрадей, 1 клетка = 5 мм. Впрочем, китайцы подпортили стандарт :) Используя ту же теорему Пифагора, легко получить формулы обратного перехода – от декартовой к полярной системе: поскольку После подробного разбора полётов с отдельно взятыми точками перейдём к закономерному продолжению темы:
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников»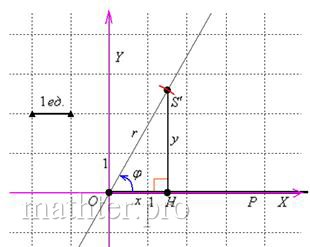 Установим взаимосвязь полярных
Установим взаимосвязь полярных 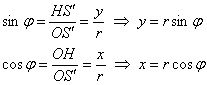
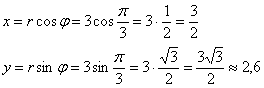
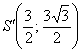
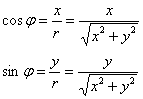 , откуда легко найти угол
, откуда легко найти угол  4.4. Уравнение линии в полярных координатах
4.4. Уравнение линии в полярных координатах 4.2. Порядок и техника построения точек в полярных координатах
4.2. Порядок и техника построения точек в полярных координатах