|
Ваш репетитор, справочник и друг!
|
4.5. Полярная розаСовершенно верно, речь пойдёт о цветке с лепестками: Задача 118 Построить линии, заданные уравнениями в полярных координатах а) Существует два подхода к построению полярной розы. Сначала пойдём по накатанной колее, считая, что полярный радиус не может быть отрицательным: Решение: а) Найдём область определения функции: Неравенство решим графически. Согласно геометрическим преобразованиям графиков, если
аргумент функции умножить на Неравенству Возможно, некоторым читателям более лёгким покажется аналитический способ нахождения области определения, условно назову его «нарезка круглого
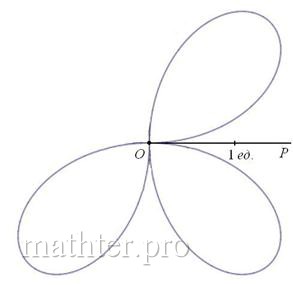
пирога». Резать будем на равные части и, прежде всего, найдём границы первого куска. Рассуждаем Разделив все части двойного неравенства на 2, получаем искомый промежуток: – найденный отрезок Прямо, как по ромашке – «любит, не любит, любит, не любит» =) С тем отличием, что тут не гадание. …Да, прямо какая-то любовь по-китайски получается…. Итак, И слева вы видите закономерный результат заботливого садовника. Следует отметить, что длину лепестка легко сразу усмотреть из уравнения
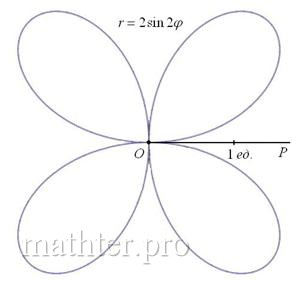
б) Построим линию, заданную уравнением – отрезок Таким образом, область определения: Построение. Если в предыдущем пункте всё благополучно обошлось прямыми углами и углами в 45 градусов, то здесь придётся немного повозиться. Найдём вершины лепестков. Их длина Чертёж желательно разметить на 60-градусные секторы (отграничены зелёными линиями) и провести направления вершин лепестков (серые линии). Сами вершины удобно наметить с помощью циркуля – единожды отмерить по линейке расстояние в 2 единицы и нанести три засечки на прочерченных направлениях в 30, 150 и 270 градусов. Понимаю, что занятие хлопотное, но если хотите всё оформить по уму, то придётся потратить время.
Сформулируем общую формулу: уравнение вида Например, уравнение О втором подходе я хотел вообще умолчать, однако не могу пройти мимо – уж слишком он распространён. Суть состоит в том, что полярная роза часто рассматривается в обобщённых полярных координатах, где полярный радиус может быть отрицательным. Вопрос области определения отпадает, но появляются другие приколы. Во-первых, разберёмся, как строить точки с отрицательным значением «эр». Если И, соответственно, когда угол проходит значения Интересно отметить, что при таком подходе роза с нечётным количеством лепестков, в частности, роза
Сформулируем правило розы для обобщенной системы координат: уравнение вида Например, роза А почему закономерность столь необычна, я только что проиллюстрировал выше. Какую систему выбрать, «классическую» или обобщённую? Зависит от вашего учебного плана. «По умолчанию» я бы особо не рекомендовал использовать обобщенные полярные координаты, ибо, зачем вам лишние вопросы со стороны преподавателя? Похожая задача для самостоятельного решения: Задача 119 Построить линии, заданные уравнением в полярных координатах Сформулировать общее правило о количестве и длине лепестков полярной розы вида В образце приведено решение в «классической» полярной системе. Повторим схему решения: – Сначала находим область определения. При этом для лучшего понимания своих действий постарайтесь соотнести аналитический способ «нарезки» с
графической интерпретацией. По материалам статьи геометрические преобразования графиков выясните, как выглядят, и при необходимости начертите графики функций – Находим угловые координаты вершин лепестков – они расположены ровно посередине промежутков области определения. – Выполняем чертёж. Пойдёт схематическая версия, однако желательно разметить найденные секторы и угловые направления вершин лепестков (в случае необходимости – с помощью транспортира). Вершины удобно засекать циркулем, предварительно установив раствор, равный длине лепестка. Существуют более солидные и общие формулы окружности, полярной розы и желающие могут с ними ознакомиться в других источниках информации. Я лишь ограничился практически значимыми (с моей точки зрения) примерами. И сейчас мы систематизируем алгоритм построения линий в полярной системе координат, и что немаловажно, значительно ускорим решение:
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников»
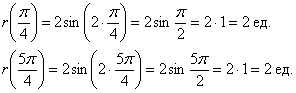
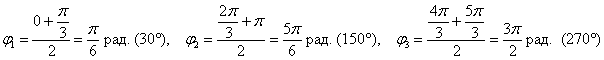 а
а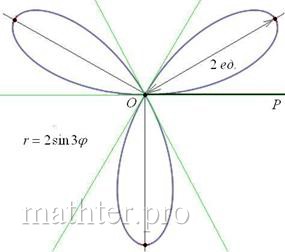
 4.6. Как построить линию в полярных координатах?
4.6. Как построить линию в полярных координатах? 4.4. Уравнение линии в полярных координатах
4.4. Уравнение линии в полярных координатах