2.1. Дискретный вариационный ряд

Пусть количественная величина может принимать лишь отдельные изолированные значения (т.е. множество значений дискретно (прерывно)).

Дискретный вариационный ряд (ДВР) – это упорядоченное по возрастанию дискретное множество вариант и соответствующие им частоты либо относительные частоты.

Частоты выборочной совокупности обозначают через , а частоты генеральной совокупности – через . Как вариант, вместо частот используют относительные частоты, они рассчитывается по формулам:

– для выборочной совокупности: , где – объем выборки,

– и буквы совокупности генеральной: , где – её объем.

Легко видеть, что сумма всех относительных частот совокупности равна единице:
, .

Всегда проверяйте этот факт! Если в сумме не единица, то либо вы ошиблись, либо в условии задачи опечатка и решить её невозможно (корректным образом).

За примером ДВР далеко ходить не будем, студенческая группа объёма :

где варианты – это упорядоченные по возрастанию оценки по матанализу (отдельные изолированные значения), а частоты – это количество студентов, получивших ту или иную оценку. Упорядоченный вариационный ряд также называют статистическим распределением совокупности. Ибо вот так вот распределены оценки.

Для разминки найдём относительные частоты:

и непременно проконтролируем, что:
.

Все вычисления обычно проводят на калькуляторе либо в Экселе (MS Excel), а результаты заносят в таблицу, при этом в статистике данные чаще располагают не в строках, а в столбцах:

Такое расположение обусловлено тем, что количество вариант может быть достаточно велико, и они просто не вместятся в стандартную строку. Не редкость, когда их 10-20, а бывает и 100-200. Но мы осилим любое количество!

Откуда берутся дискретные вариационные ряды? Они появляются в результате исследования дискретной характеристики статистической совокупности, причём, варианты ряда не отличаются большим разнообразием. Например, оценки (коих не так много) в примере выше. И чтобы составить вариационный ряд, ещё нужно потрудиться:

Пример 4

По результатам выборочного исследования рабочих цеха были установлены их квалификационные разряды: 4, 5, 6, 4, 4, 2, 3, 5, 4, 4, 5, 2, 3, 3, 4, 5, 5, 2, 3, 6, 5, 4, 6, 4, 3.

Требуется: составить вариационный ряд и построить полигон частот; найти относительные частоты и построить эмпирическую функцию распределения.

Решение: в условии прямо сказано о том, что перед нами выборка из генеральной совокупности (всех рабочих цеха), и первое, что логично сделать – подсчитать её объем, т.е. количество рабочих. Здесь это легко сделать устно, циферок в условии: .

Квалификационные разряды – есть величина дискретная и этих разрядов немного. Поэтому нам предстоит составить дискретный вариационный ряд (обратите внимание, что в условии ничего не сказано о характере ряда).

Как составить дискретный вариационный ряд?

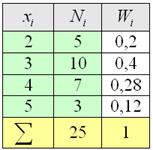
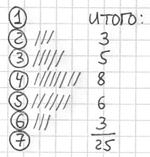
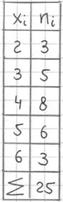
Если у вас под рукой нет программ, то вручную. При этом оптимальным может быть следующий алгоритм: сначала окидываем взглядом все числа и определяем среди них минимальное (примерно) и максимальное (примерно). В данном случае ориентировочный диапазон – от 1 до 7. Записываем их в столбец на черновике и обводим в кружочки. Далее начинаем вычёркивать карандашом числа из исходного списка:

и делать засечки около соответствующих кружков:

После того, как все числа будут вычеркнуты, подсчитываем количество засечек в каждой строке:

Обязательно проверяем, получается ли у нас в сумме объём выборки:
– отлично!

Заносим найденные значения в таблицу на чистовик:

…ну что же, вполне и вполне логично – рабочих средней квалификации много, а учеников и мастеров – мало. Полученные результаты позволяются достаточно точно судить об уровне квалификации всего цеха (если, конечно, выборка представительна)

Дискретный вариационный ряд можно изобразить графически:

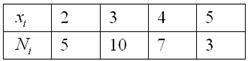
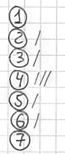
2.1.1. Полигон распределения

2. Вариационные ряды

| Оглавление |