2.1.1. Полигон распределения

Полигон частот – это ломаная, соединяющая соседние точки :

Кстати, с помощью полигона можно не только изобразить, но ещё и однозначно задать дискретный вариационный ряд (вместо таблицы с вариантами и частотами).

Теперь программный способ решения:

Задание

Самостоятельно решить данную задачу в Экселе (прямо в открывшемся файле).

Решаем! – все исходные данные с пошаговыми инструкциями прилагаются.

После чего переходим ко второй части задачи, в которой требуется найти относительные частоты и построить эмпирическую функцию распределения.

Относительные частоты рассчитываем по формуле – для этого каждую частоту делим на объём выборки и результаты заносим в дополнительный столбец, далее я перехожу к электронной версии оформления:

Обязательно проверяем, что сумма всех относительных частот равна единице:
, ОК.

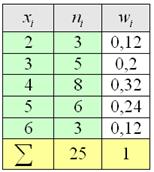
Иногда требуется построить полигон относительных частот. Как вы правильно догадались – это ломаная, соединяющая соседние точки . Но такое задание больше характерно для интервального вариационного ряда, до которого мы доберёмся в самом близком будущем.

А теперь посмотрим на относительные частоты и задумаемся: на что они похожи? …Правильно, на вероятности. Так, например, можно сказать, что – есть примерная вероятность того, что наугад выбранный рабочий цеха будет иметь 4-й разряд. «Примерная» – по той причине, что перед нами выборка. А вот учесть ВСЕХ рабочих цеха (всю генеральную совокупность), то рассчитанные относительные частоты – в точности и есть эти вероятности.

Полигон относительных частот – это статистический аналог многоугольника распределения из теории вероятностей. Следует заметить, что он уже не задаёт вариационный ряд, так как относительные частоты (сами по себе) ничего не говорят нам о частотах и объеме совокупности.

Но не полигоном единым жив дискретный вариационный ряд, существует и другой подход к его заданию и изображению:

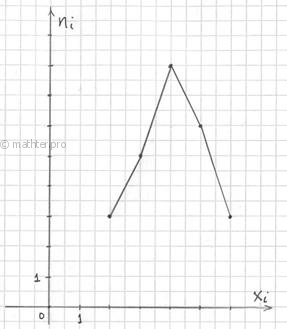
2.1.2. Эмпирическая функция распределения

2.1. Дискретный вариационный ряд

| Оглавление |