Ваш репетитор, справочник и друг!

Математическая статистика – краткий курс для начинающих

2.2. Интервальный вариационный ряд

Предпосылкой построения интервального вариационного ряда (ИВР) является тот факт, что исследуемая величина принимает слишком много различных значений . Зачастую ИВР появляется в результате изучения непрерывной характеристики объектов. Типично – это время, масса, размеры и другие физические величины. Вспоминаем Константина, который замерял время на лабораторной работе и Фёдора, который взвешивал помидоры.

В таких ситуациях затруднительно либо невозможно применить тот же подход, что для дискретного ряда. Это связано с тем, что ВСЕ варианты различны (во многих случаях). И даже если встречаются совпадающие значения, например, 50 грамм и 50 грамм, то связано это с округлением, а фактически значения всё равно отличаются хоть какими-то микрограммами.

Поэтому здесь используется другой подход, а именно определяется интервал,
в пределах которого варьируются значения , затем этот интервал делится на частичные интервалы (обычно равной длины ) и по каждому частичному интервалу подсчитываются частоты (либо ) – количество вариант, которые в него попали.
Если варианта попала на «стык» интервалов, то её относят к старшему интервалу.

Интервальный вариационный ряд (ИВР) статистической совокупности – это упорядоченное множество смежных интервалов и соответствующие им частоты, в сумме равные объёму совокупности. Дабы не плодить лишних букв и индексов, я никак не обозначил эти интервалы. Придирчивый читатель, к слову, наверняка заметил, что через я обозначаю как исходные варианты, так и значения сгруппированного ряда.

Следует отметить, что исследуемая характеристика не обязана быть непрерывной, и мы как раз начнём с такой задачи:

Пример 6

По результатам исследования цены некоторого товара в различных торговых точках города, получены следующие данные (в денежных единицах):

Составить вариационный ряд, построить гистограмму частот, гистограмму и полигон относительных частот + бонус: эмпирическую функцию распределения.

Решение: очевидно, что перед нами выборочная совокупность объема , и вопрос номер один: какой ряд составлять – дискретный или интервальный? Заметьте, что в вопросе задачи ничего не сказано о характере ряда. Строго говоря, цены дискретны и среди них даже есть одинаковые. Однако они могут быть округлены, да и разброс цен довольно велик. Поэтому здесь целесообразно провести интервальное разбиение.

Начнём с экстремальной ситуации, когда у вас под рукой нет Экселя или другого подходящего программного обеспечения. Только ручка, карандаш, тетрадь и калькулятор.

Тактика действий похожа на работу с дискретным вариационным рядом. Сначала окидываем взглядом предложенные числа и определяем примерный интервал, в который вписываются эти значения. «Навскидку» все значения заключены в пределах от 5 до 11. Далее делим этот интервал на удобные подынтервалы, в данном случае напрашиваются промежутки единичной длины. Записываем их на черновик:

Теперь начинаем вычёркивать числа из исходного списка и записываем их в соответствующие колонки нашей импровизированной таблицы:

После этого находим самое маленькое число в левой колонке (минимальное значение) и самое большое число – в правой (максимальное значение). Тут даже ничего искать не пришлось, честное слово, не нарочно получилось:)
ден. ед. – не забываем указывать размерность!

Вычислим размах вариации:
ден. ед. – длина общего интервала, в пределах которого варьируется цена.

Теперь его нужно разбить на частичные интервалы. Сколько интервалов рассмотреть? По умолчанию на этот счёт существует формула Стерджеса:

, где – десятичный логарифм* от объёма выборки и
– оптимальное количество интервалов, при этом результат округляют до ближайшего левого целого значения.

* есть на любом более или менее приличном калькуляторе.

В нашем случае получаем: интервалов.

Следует отметить, что правило Стерджеса носит рекомендательный, но не обязательный характер. Нередко в условии задачи прямо сказано, на какое количество интервалов следует проводить разбиение (на 4, 5, 6, 10 и т.д.), и тогда следует придерживаться именно этого указания.

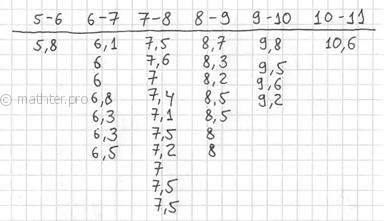
Длины частичных интервалов могут быть различны, но в большинстве случаев использует равноинтервальную группировку:
– длина частичного интервала. В принципе, здесь можно было не округлять и использовать длину 0,96, но удобнее, ясен день, 1.

И коль скоро мы прибавили 0,04, то по пяти частичным интервалам получается «перебор»: . Посему от самой малой варианты отмеряем влево 0,1 влево (половину «перебора») и к значению 5,7 начинаем прибавлять по , получая тем самым частичные интервалы. При этом сразу рассчитываем их середины (например, ) – они требуются почти во всех тематических задачах:

– убеждаемся в том, что самая большая варианта вписалась в последний частичный интервал и отстоит от его правого конца на 0,1.

Далее подсчитываем частоты по каждому интервалу. Для этого в черновой таблице обводим значения, попавшие в тот или иной интервал, подсчитываем их количество и вычёркиваем:

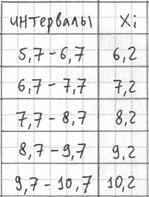
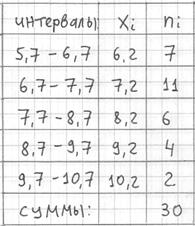
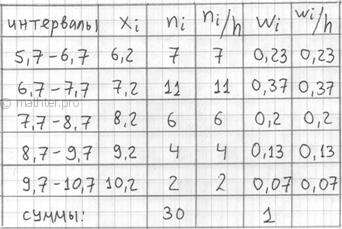
Так, значения из 1-го интервала я обвёл овалами (7 штук) и вычеркнул, значения из 2-го интервала – прямоугольниками (11 штук) и вычеркнул и так далее. Варианта попала на «стык» интервалов и, согласно озвученному выше правилу, её следует отнести к последующему интервалу .

В результате получаем интервальный вариационный ряд:

при этом обязательно убеждаемся в том, что ничего не потеряно:
, ОК.

…Да, кстати, все ли представили свой любимый товар, чтобы было интереснее разбирать это длинное решение? J

Точно также как и в дискретном случае, интервальный вариационный ряд можно
(и нужно) изобразить графически. И здесь у нас весьма большое разнообразие. Но сначала добавим в таблицу дополнительные столбцы и продолжим расчёты:

По каждому интервалу рассчитываем (не тушуемся): плотность частот , относительные частоты (округляем их до 2 знаков после запятой), а также плотность относительных частот . Поскольку длина частичного интервала , то вычисления заметно упрощаются:

Если интервалы имеют разные длины , то при нахождении плотностей каждую частоту нужно разделить на длину своего интервала: . Но у нас группировка равноинтервальная, да не абы какая, а с единичным частичным интервалом. Дело за чертежами. Один за другим:

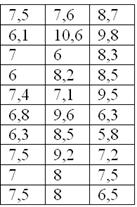
2.2.1. Гистограммы

2.1.2. Эмпирическая функция распределения

| Оглавление |