2.1.2. Эмпирическая функция распределения
Это статистический аналог функции
распределения из теорвера. Данная функция определяется, как отношение:
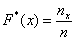 , где , где 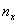 – количество вариант СТРОГО МЕНЬШИХ, чем – количество вариант СТРОГО МЕНЬШИХ, чем 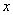 , ,
при этом «икс» «пробегает» все значения от «минус» до «плюс» бесконечности.
Построим эмпирическую функцию распределения 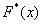 для нашей задачи. Чтобы было нагляднее, отложу варианты для нашей задачи. Чтобы было нагляднее, отложу варианты 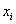 и их количество и их количество 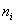 на числовой оси: на числовой оси:

На интервале 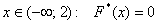 – по той причине, что
левее ЛЮБОЙ точки этого интервала вариант – по той причине, что
левее ЛЮБОЙ точки этого интервала вариант 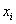 нет. Кроме того, функция равна нулю ещё и в точке нет. Кроме того, функция равна нулю ещё и в точке 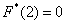 . Почему? Потому, что значение . Почему? Потому, что значение 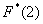 определяет количество вариант (см. определение), которые
СТРОГО меньше двух, а это количество равно нулю. определяет количество вариант (см. определение), которые
СТРОГО меньше двух, а это количество равно нулю.
На промежутке 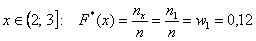 – и опять обратите
внимание, что значение – и опять обратите
внимание, что значение 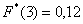 не учитывает
рабочих 3-го разряда, т.к. речь идёт о вариантах, которые СТРОГО меньше трёх (по определению). не учитывает
рабочих 3-го разряда, т.к. речь идёт о вариантах, которые СТРОГО меньше трёх (по определению).
На промежутке 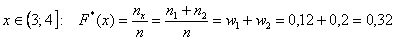 – и далее процесс
продолжается по принципу накопления частот: – и далее процесс
продолжается по принципу накопления частот:
– если 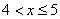 , то , то 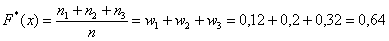 ; ;
– если 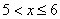 , то , то 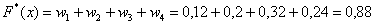 ; ;
– и, наконец, если 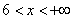 , то , то 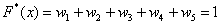 – и в самом деле, для ЛЮБОГО «икс» из интервала – и в самом деле, для ЛЮБОГО «икс» из интервала 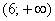 ВСЕ частоты ВСЕ частоты 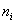 расположены СТРОГО левее этого значения «икс» (см.
чертёж выше). расположены СТРОГО левее этого значения «икс» (см.
чертёж выше).
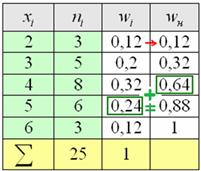
Накопленные относительные частоты 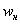 удобно заносить в отдельный столбец таблицы, при этом алгоритм вычислений очень
прост: сначала сносим слева частоту удобно заносить в отдельный столбец таблицы, при этом алгоритм вычислений очень
прост: сначала сносим слева частоту 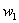 (красная стрелка), и каждое следующее значение (красная стрелка), и каждое следующее значение 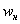 получаем как сумму предыдущего и относительной
частоты из текущего левого столбца (зелёные обозначения): получаем как сумму предыдущего и относительной
частоты из текущего левого столбца (зелёные обозначения):
Вот ещё, кстати, один довод за вертикальную ориентацию данных – справа по надобности можно приписывать дополнительные
столбцы.
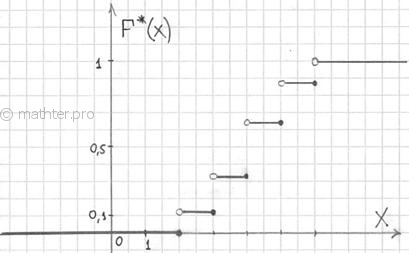
Построенную функцию принято записывать в кусочном виде:

а её график представляет собой ступенчатую фигуру:
Эмпирическая функция распределения не убывает и принимает значения лишь из промежутка 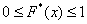 , и если у вас вдруг получится что-то не так, то ищите ошибку. , и если у вас вдруг получится что-то не так, то ищите ошибку.
Теперь смотрим видео, о том, как построить эту функцию в Экселе
(Ютуб).
И, конечно, вспомним основной метод математической статистики.
Эмпирическая функция распределения 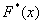 строится по выборке и приближает теоретическую функцию распределения строится по выборке и приближает теоретическую функцию распределения 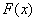 . Легко догадаться, что последняя появляется в
результате исследования всей генеральной совокупности, но если рабочих в цехе ещё пересчитать можно, то звёзды на
небе – уже вряд ли. Вот поэтому и важнА функция эмпирическая, и ещё важнее, чтобы выборка была
репрезентативна, дабы приближение было хорошим. . Легко догадаться, что последняя появляется в
результате исследования всей генеральной совокупности, но если рабочих в цехе ещё пересчитать можно, то звёзды на
небе – уже вряд ли. Вот поэтому и важнА функция эмпирическая, и ещё важнее, чтобы выборка была
репрезентативна, дабы приближение было хорошим.
Миниатюрное задание для закрепления материала:
Пример 5
Дано статистическое распределение совокупности:
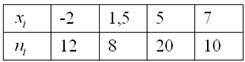
Составить эмпирическую функцию распределения, выполнить чертёж
Решаем самостоятельно – все числа уже в Экселе! Свериться с образцом можно в конце
книги. По поводу красоты чертежа сильно не запаривайтесь, главное, чтобы было правильно – этого обычно достаточно для
зачёта.
 2.2. Интервальный вариационный ряд 2.2. Интервальный вариационный ряд
 2.1.1. Полигон распределения 2.1.1. Полигон распределения
| Оглавление |
|

 Математическая статистика – краткий курс для начинающих
Математическая статистика – краткий курс для начинающих




 2.2. Интервальный вариационный ряд
2.2. Интервальный вариационный ряд 2.1.1. Полигон распределения
2.1.1. Полигон распределения