2.2.1. Гистограмма частот

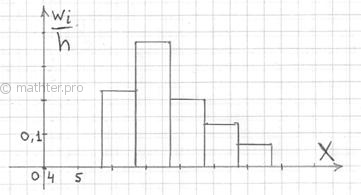
– это фигура, состоящая из прямоугольников, ширина которых равна длинам частичных интервалов (данные задачи), а высота – соответствующим плотностям частот:

при этом вполне допустимо использовать нестандартную шкалу по оси абсцисс, в данном случае я начал нумерацию с четырёх. Площадь гистограммы частот в точности равна объёму совокупности: . В нашем случае и плотности совпали с самими частотами , таким образом:

2.2.2. Гистограмма относительных частот

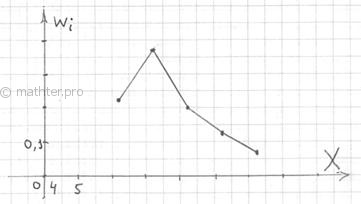
– это фигура, состоящая из прямоугольников, ширина которых равна длинам частичных интервалов, а высота – соответствующим плотностям относительных частот:

Площадь такой гистограммы равна единице: , и это статистический аналог функции плотности распределения непрерывной случайной величины.

Построенный чертёж даёт наглядное и весьма точное представление о распределении цен на ботинки по всей генеральной совокупности. При условии, что выборка представительна.

И для ИВР чаще всего требуется построить гистограмму именно относительных частот. А вместе с ней нередко и полигон таковых частот. Без проблем, полигон относительных частот – это ломаная, соединяющая соседние точки , где – середины интервалов:

По сути, здесь мы приблизили интервальный ряд дискретным, выбрав в качестве вариант середины интервалов. Это важнейший принцип и метод, который неоднократно встретится нам в будущем.

Большим достоинством приведённого решения является тот факт, что многие вычисления здесь устные, а если вы помните, как делить «столбиком», то можно обойтись даже без калькулятора. Вот она где притаилась, смерть Терминатора :) ;)

Автоматизируем решение в Экселе (видео на Ютуб).

И бонус:

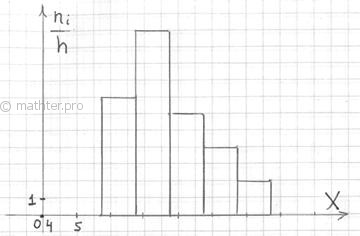
2.2.3. Эмпирическая функция распределения интервального ряда

2.2. Интервальный вариационный ряд

| Оглавление |