2.2.3. Эмпирическая функция распределения интервального ряда

Она определяется точно так же, как в дискретном случае:

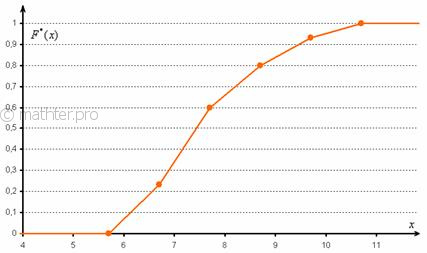
, где – количество вариант СТРОГО МЕНЬШИХ, чем «икс», который «пробегает» все значения от «минус» до «плюс» бесконечности.

Но вот построить её для интервального ряда намного проще. Находим накопленные относительные частоты:

И строим кусочно-ломаную линию, с промежуточными точками , где – правые концы интервалов, а – относительная частота, которая успела накопиться на всех «пройденных» интервалах:

При этом если и если .

Напоминаю, что данная функция не убывает, принимает значения из промежутка и, кроме того, для ИВР она ещё и непрерывна.

Эмпирическая функция является аналогом функции распределения НСВ и приближает теоретическую функцию , которую теоретически, а иногда и практически можно построить по всей генеральной совокупности.

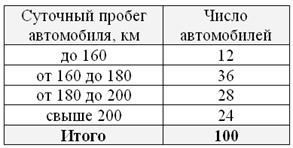
Помимо перечисленных графиков, вариационные ряды также можно представить с помощью кумуляты и огивычастот либо относительных частот, но в классическом учебном курсе эта дичь редкая, и поэтому я не буду останавливаться на ней этой книге. Скажу только, что у вас вряд ли возникнут проблемы с их построением в случае такой необходимости.
Теперь что касаемо объёма выборки. Хорошо, если в вашей задаче всего лишь 20-30-50 вариант, но что делать, если их 100-200 и больше? В моей практике встречались десятки таких задач, и ручной подсчёт здесь уже не торт. Никаких проблем:

Как быстро составить ИВР при большом объёме выборки? (Ютуб)

Но не всё так сурово. Во многих задачах вам будет дан готовый вариационный ряд:

Пример 7

Выборочная проверка партии чая, поступившего в торговую сеть, дала следующие результаты:

Требуется построить гистограмму и полигон относительных частот, эмпирическую функцию распределения

Проверяем свои навыки работы в Экселе! (исходные числа и краткая инструкция прилагается) И на всякий случай краткое решение для сверки есть в конце книги.

Иногда встречаются ИВР с открытыми крайними интервалами, например:

В таких случаях интервалы «закрывают». Обычно поступают так: сначала смотрим на средние интервалы и выясняем длину частичного интервала: км. И для дальнейшего решения можно считать, что крайние интервалы имеют такую же длину: от 140 до 160 и от 200 до 220 км. Соответственно, середины интервалов: 150 и 210 км.

И самое важное по главе, обязательно прочитайте, тут немного:)

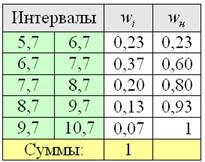
2.3. Вариационные ряды – главное

2.2.2. Гистограммы

| Оглавление |