|
Ваш репетитор, справочник и друг!
|
3.1. Показатели центральной тенденцииПростейший пример такого показателя нам уже встречался – это среднее арифметическое значение. Но средней дело не ограничивается, впрочем, обо всём по порядку: 3.1.1. Генеральная и выборочная средняяПусть исследуется некоторая генеральная совокупность объёма Генеральной средней называют среднее арифметическое всех значений этой совокупности: Если среди чисел Живой пример вычисления генеральной средней встретился в Примере 2, но чтобы не занудничать, я даже не буду напоминать его содержание. Далее. Как мы помним, обработка всей генеральной совокупности часто затруднена либо невозможна, и поэтому из неё организуют представительную выборку объема Выборочной средней называется среднее арифметическое всех значений выборки: Выборочная средняя Практику начнём с дискретного вариационного ряда и знакомого условия: Пример 8 По результатам выборочного исследования Это числа из Примера 4, но теперь нам требуется: вычислить выборочную среднюю, и, не отходя от станка, найти моду и медиану. Как решать задачу? Если нам даны первичные данные (конкретные варианты Но здесь удобнее составить вариационный ряд:
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Математическая статистика – краткий курс для начинающих
Математическая статистика – краткий курс для начинающих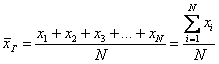
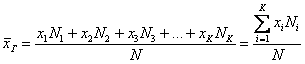 , где:
, где: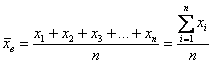
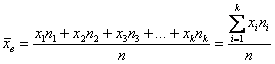 – как сумма произведений вариант
– как сумма произведений вариант 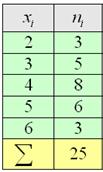
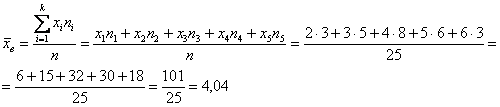
 3.1.2. Мода
3.1.2. Мода  3. Основные показатели статистической совокупности
3. Основные показатели статистической совокупности