|
Ваш репетитор, справочник и друг!
|
6.4. Аналитическая группировкаДанная группировка позволяет установить наличие и характер зависимости одного вариационного ряда от другого. Это может быть связь между признаками разных статистических совокупностей или (что чаще) между признаками одной совокупности: Пример 42 Имеются выборочные данные о выпуске продукции (млн. руб.) и прибыли (млн. руб.) по 30 предприятиям за некоторый
период: Методом аналитической группировки установить наличие и характер зависимости между стоимостью произведенной продукции и средней прибылью предприятий. Результаты оформить в виде групповой и аналитической таблицы. Сделать выводы, куда ж без них. Итак, по условию нам дано два вариационных ряда: Такая нежёсткая зависимость называется корреляционной. Это зависимость, при которой изменение одного показателя влечёт изменение СРЕДНИХ значений другого показателя. Этим корреляционная зависимость отличается от функциональной, где изменение аргумента оказывает чёткое и безусловное влияние на изменение функции. Показатель Но не всё так просто. Дело в том, что вышесказанное является лишь нашим предположением. А вдруг в условии дано 30 каких-нибудь северокорейских заводов, где нет такой зависимости? Именно поэтому по условию нужно установить наличие зависимости между выпуском продукции и прибылью и определить её характер. Под характером понимается корреляционность зависимости и её направление, при этом возможны следующие варианты: – прямая связь («чем больше, тем больше» – наш случай); И установить всё это нужно методом аналитической группировки, которая позволяет выявить наличие (либо
отсутствие) и направление корреляционной связи между признаком-фактором И мы начинаем, наконец, оформлять решение: Прежде всего, нужно определить признак-фактор и признак-результат. Самостоятельно, на основе логических рассуждений. Тут же высказываем предположение о наличии и направлении предполагаемой корреляционной связи. В нашей задаче можно записать примерно следующее: Очевидно, что средний размер прибыли по предприятиям зависит от стоимости выпущенной продукции, при этом, чем
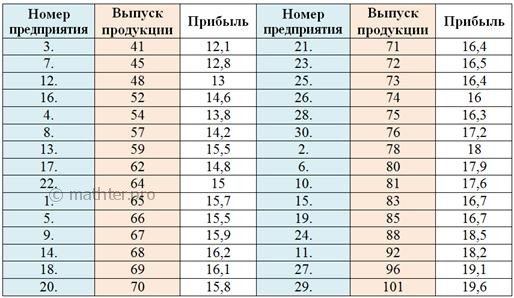
больше выпущено продукции, тем выше может быть прибыль. Таким образом, выпуск продукции Обращаю ваше внимание, что данная часть задания является если не обязательной, то строго желательной. Часто в условии прямо запрашивается этот пункт. Теперь проверяем нашу гипотезу (предположение) методом аналитической группировки. Сначала нужно упорядочить совокупность по признаку-фактору. Расположим предприятия по возрастанию выпуска
продукции (оранжевый цвет): В Экселе эта сортировка выполняется буквально в пару щелчков, и чуть ниже будет ролик о том, как быстро решить нашу задачу. Номера предприятий можно было опустить, но я оставил их для лучшего понимания выполненного действия. Заметьте, что зависимый показатель является ведомым, это означает, что числа в колонке «Прибыль» переместились вслед за числами в колонке «Выпуск продукции». Теперь выполняем группировку совокупности – опять же по признаку-фактору (выпуску продукции). Поскольку в условии нет никаких указаний на этот счёт, то используем стандартную равноинтервальную группировку. Размах вариации составляет: Оптимальное количество интервалов определим по формуле Стерджеса, для объёма совокупности
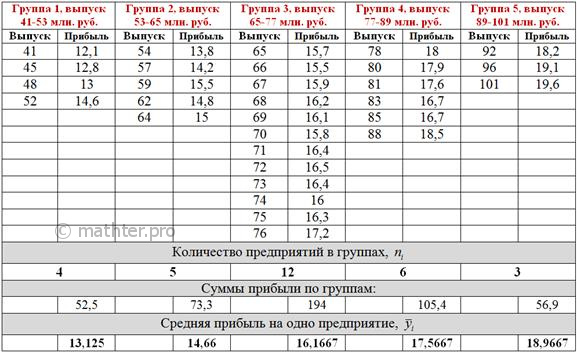
Таким образом, длина каждого интервала: 41-53, 53-65, 65-77, 77-89 и 89-101 млн. руб. Собственно, разносим предприятия по группам и начинаем заполнять групповую
таблицу. Напоминаю, что значения, попадающие на «стык» интервалов следует относить в следующий интервал: В нижней части таблицы подсчитываем количество Основные результаты представим в виде аналитической таблицы: Теперь смотрим короткое видео о том, как это всё быстро подсчитать. Сделаем краткие выводы: аналитическая группировка показала, что при увеличении стоимости выпущенной продукции наблюдается увеличение средней прибыли по предприятиям. Таким образом, между рассмотренными факторами действительно существует прямая корреляционная зависимость. Таким образом, наше предположение (см. начало задания) подтвердилось. Обращаю внимание, что средние значения (правая колонка) не обязаны строго возрастать (либо убывать), и если вы получите такой результат, то это будет нормально, ведь корреляционная зависимость не является жёсткой. ВажнА общая тенденция увеличения (либо уменьшения) средних значений. Но может статься, что по итогу вообще не проучится какой-то внятной закономерности. И это тоже результат исследования! С соответствующими выводами о слабой коррел. зависимости либо отсутствии таковой. И здесь возникает закономерный вопрос: а насколько СИЛЬНО влияет факторный признак на результат, насколько теснА
связь между факторами? На этот вопрос отвечают специальные статические показатели, о которых я
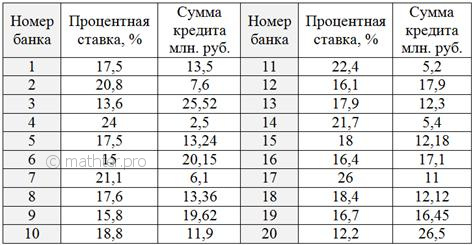
рассказал на сайте. По причине редкости этой не самой простой задачи она не вошла в эту книгу. Пример 43 По результатам выборочного исследования 20 банков известны процентные ставки и соответствующие суммы выданных
кредитов: Требуется: Обратите внимание, что во 2-м пункте вам прямо указано, как следует выполнять группировку – в таких случаях не нужно проявлять самодеятельность – строго следуем указаниям условия. А если решение получится не слишком удачное, то это уже проблемы автора задачи. Все числа забиты в Эксель и вам осталось быстренько выполнить действия. Решение для сверки в конце книги. Что ещё можно сказать по теме? В некоторых задачах результативных признаков может быть несколько, как правило, два, например: И в заключение параграфа хочу сказать, что показатели вам могут быть предложены самые разные, поэтому при решении подобных задач следует «включать голову» и элементарную логику.
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Математическая статистика – краткий курс для начинающих
Математическая статистика – краткий курс для начинающих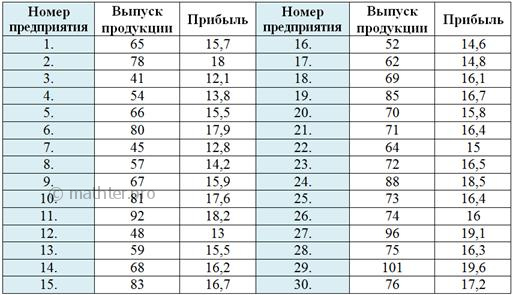

 6.5. Комбинационная группировка
6.5. Комбинационная группировка 6.3. Перегруппировка
6.3. Перегруппировка