Ваш репетитор, справочник и друг!

Математическая статистика – краткий курс для начинающих

6.5. Комбинационная группировка

Комбинационная группировка – это группировка статистической совокупности совместно по двум или бОльшему количеству признаков. Она позволяет выявить устройство совокупности и установить взаимосвязи между её признаками.

Рассмотрим выборку, состоящую из котов, среди которых оказалось 20 грациозных (менее 4 кг), 50 обычных (4-6 кг) и 30 толстых (более 6 кг). По существу, перед нами структурная группировка животных по их массе, и это первый признак статической совокупности. Теперь возьмём какой-нибудь второй признак, например, разделим всех котов на злых и добрых :) Признак, кстати, качественный, но при желании его можно «оцифровать», рассмотрев некую экспертную шкалу доброты.

В результате исследования выяснилось, что среди тощих котов 14 злых и 6 добрых, среди обычных – 24 злых и 26 добрых и среди толстых – 7 злых и 23 добрых.

Очевидно, что между этими признаками есть связь. Чем больше масса кота, тем более вероятно, что он окажется добрым. Ибо с лишним весом, полным желудком и отрезанн … злиться весьма проблематично. Однако и среди толстых котов тоже есть особи с проблемным характером. Такая нежёсткая зависимость называется…, вспоминаем… – правильно! Корреляционной.

Полученные данные обычно сводят в комбинационную таблицу:

Внимательно изучаем таблицу и обозначения! Это очень, ОЧЕНЬ важно для практики:

1) Признак-фактор (причину) и его категории располагают в левом столбце (зелёный цвет), а признак-результат (следствие) и его категории – в «шапке» таблицы (жёлтый цвет). Встречается и расположение наоборот (что с моей точки зрения удобнее), но в практических задачах почему-то в ходу первый вариант. Но мы не будем комплексовать, попробуем и так, и так.

2) В основной части таблицы (серый цвет) располагаются собственно результаты группировки – совместные групповые частоты . Итак, у нас в наличии есть:
тощих и злых и тощих и добрых котов;
обычных и злых и обычных и добрых котов;
толстых и злых и толстых и добрых котов;

Итого: 6 групп.

! Справка: первый подстрочный индекс означает номер строки (рассматриваем серую область), а второй – номер столбца. Так, значение, расположено в 1-й строке, 2-м столбце, а значение – в 3-й строке, 1-м столбце.

Сумма всех групповых частот равна объёму статистической совокупности:

! Справка: значок двойного суммирования работает следующим образом: сначала переменная «и» принимает значение и переменная «жи» пробегает все свои значения (от 1 до 2), в результате чего получается сумма . Затем первая переменная принимает значение и «жи» снова пробегает все свои значения: . И, наконец, для получаем сумму .

Часто для краткости пишут или даже используют одинарный значок суммы:

Заканчиваем разбор таблицы:

3) В правом столбце (зелёный цвет) располагаются суммы по строкам (по группам признака-фактора). В нашей совокупности имеется грациозных, обычных и толстых котов. Итого: особей.

В нижней строке (жёлтый цвет) подсчитываем суммы по столбцам (по категориям признака-результата): злых и добрых котов. Итого: , в чём и требовалось убедиться.

Общая котосумма (объём совокупности) находится в правом нижнем углу: .

Если вы что-то не очень поняли,
то ещё раз ВДУМЧИВО перечитайте объяснения!

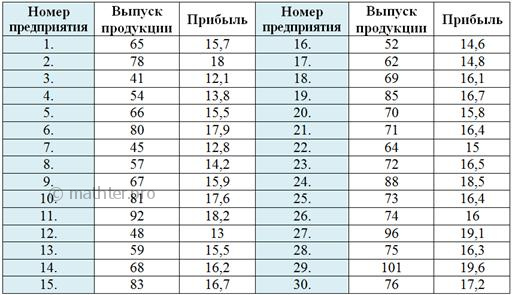
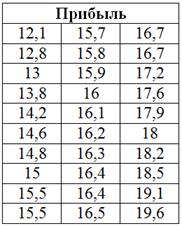
Может ли в комбинационной группировке быть бОльшее количество факторов? Легко. Так, в нашем примере можно добавить фактор – жилищные условия кота (бездомный или домашний). В результате получится трёхмерная комбинационная группировка с группами:

тощие, злые и бездомные коты;
тощие, злые и домашние коты;
тощие, добрые и бездомные коты;
тощие, добрые и домашние коты;
обычные, злые и бездомные коты;
…
и так далее, всего 12 групп. Самостоятельно перечислите и представьте все остальные семейства – целый мир получится :)

И, завершая занимательное котоведение, призываю вас не кастрировать своих (и чужих) котов и не топить котят. И мир станет гармоничнее! …Простите за отступление, Майкл Джексон любил детей, а я люблю котов. Да и студентов тоже не тяну за хвосты :)

Поэтому переходим к стандартной студенческой задаче, в которой предлагается простейшая двумерная комбинационная группировка:

Пример 44

Имеются выборочные данные о выпуске продукции (млн. руб.) и сумме прибыли (млн. руб.) по 30 предприятиям:

Определить признак-фактор и признак-результат и высказать предположение о наличии и направлении корреляционной зависимости между признаками. Выполнить комбинационную группировку, разбив значения признака-фактора на 5 равных интервалов, а значения признака-результата – на 3 интервала. Сделать выводы.

Числовые данные я взял из Примера 42, где мы выяснили, что признаком-фактором (причиной) является – выпуск продукции, а признаком-результатом (следствием) – прибыль предприятий. При увеличении выпуска продукции, очевидно, растёт средняя прибыль предприятий, таким образом, предполагаемая корреляционная зависимость – прямая («чем больше, тем больше»). И снова подчёркиваю нежёсткость этой зависимости: отдельно взятое предприятие может выпускать много, но «сидеть» в убытках, и наоборот – есть предприятия с небольшим объёмом выпуска, но высокой маржой (прибылью). Однако это всё отклонения от общей тенденции.

Начало решения совпадает с началом Примера 42. Упорядочим предприятия по возрастанию признака-фактора:

Далее мы нашли размах вариации млн. руб. и разбили значения признака-фактора на 5 равных интервалов. Длина каждого интервала составила млн. руб., после чего у нас получились следующие группы:

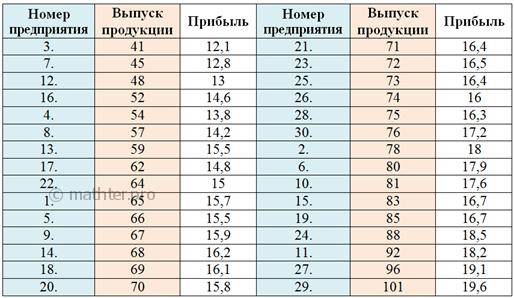
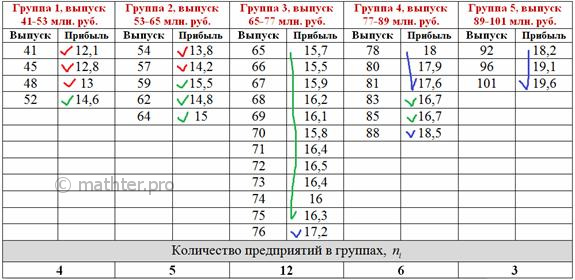
Теперь в каждой группе нужно выделить подгруппы, условно говоря, предприятия с небольшой, средней и высокой прибылью (3 интервала по условию). Для этого берём исходные значения признака-результата (прибыли) и сортируем их по возрастанию. Для компактности расположу упорядоченные значения в три колонки:

С простейшей экселевской сортировкой, полагаю, проблем уже ни у кого нет. А если таки-есть, то снова гляньте тут~~, царь тут~~. Я зануда, в полезном смысле этого слова :)

Вычислим размах вариации: млн. руб. и длину каждого интервала: ,… ай, как удачно разделилось! В результате получилось три интервала прибыли: 12,1-14,6; 14,6-17,1 и 17,1-19,6 млн. руб.

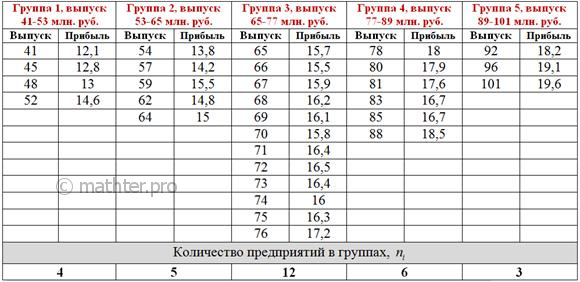
Теперь в групповой таблице красными галочками помечаем предприятия 1-го интервала, зелёными – предприятия 2-го интервала и синими – 3-го интервала:

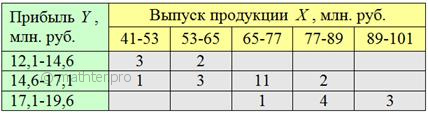
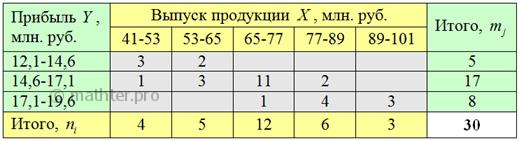
По каждой из 5 групп подсчитываем количество предприятий с небольшой (красной), средней (зелёной) и высокой (синей) прибылью. Результаты сведём в комбинационную таблицу, при этом значения признака-фактора удобно расположить по горизонтали – в «шапке» таблицы, а значения признака-результата слева по вертикали:

Следует заметить, что построение комбинационной группировки можно автоматизировать (например, в MS Excel), но в простейших учебных примерах проще выполнить ручной подсчёт частот.

Да, всем ли понятны значения (частоты) в серой области? Частота означает, что у нас есть два предприятия с выпуском продукции 53-65 млн. руб. и невысокой прибылью (12,1-14,6 млн. руб.). Частота означает, что в выборке 4 предприятия с выпуском продукции 77-89 млн. руб. и высокой прибылью (17,1-19,6 млн. руб.).

Для самоконтроля подсчитываем суммы по серым столбцам:
, всего: предприятий. Результаты заносим в нижнюю строку (см. таблицу ниже).

И самое интересное – суммы по серым строкам:
предприятий с небольшой прибылью;
предприятий со средней прибылью;
предприятий с высокой прибылью.

Итого: , что и требовалось проверить. Результаты заносим в правый столбец. Таким образом, итоговая комбинационная таблица выглядит следующим образом:

Сделаем выводы. На основании чего? Смотрим, как располагаются частоты (числа в серой области).

Если частоты имеют тенденцию располагаться по диагонали от левого верхнего до правого нижнего угла, то между признаками существует прямая корреляционная зависимость («чем больше, тем больше»). Это наш случай – по таблице хорошо видно, что с увеличением выпуска продукции растут и средние прибыли предприятий. Готово.

Если частоты имеют тенденцию располагаться по диагонали от левого нижнего до правого верхнего угла, то между признаками существует обратная корреляционная зависимость («чем больше, тем меньше»).

И, наконец, если частоты расположены хаотично, без явной закономерности, то корреляционная зависимость отсутствует либо является слабой.

И здесь опять возникает вопрос: насколько СИЛЬНО влияет признак-фактор на признак-результат. Ответ на этот вопрос дают эмпирические показатели, и один из них (линейный коэффициент корреляции) мы разберём в этой книге.

На практике в большинстве случаев вам предложат готовую комбинационную таблицу, и поэтому задания на комбинационную группировку не будет, полагаю, что в случае чего она не вызовет у вас затруднений.

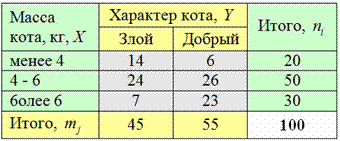
6.6. Итоги по главе

6.4. Аналитическая группировка

| Оглавление |