Ваш репетитор, справочник и друг!

Математическая статистика – краткий курс для начинающих

6.2. Структурная группировка

Напоминаю, это группировка качественно однородной совокупности по числовому признаку. Примеры только что были выше, и мы продолжаем. Суровая задача местного Политеха для студентов около- и машиностроительных специальностей:

Пример 38

В результате выборочного исследования 30 станков рассчитаны их относительные показатели металлоёмкости (т/кВт):

Требуется:
а) вычислить общую (выборочную) среднюю;
б) выполнить структурную равноинтервальную группировку;
в) выполнить структурную равнонаполненную группировку;
г) выбрать наиболее удачную группировку и вычислить выборочные средние; результаты оформить в виде групповой таблицы;
д) по выбранной группировке построить интервальный вариационный ряд;
е) сделать краткие выводы.

Но прежде, немного о содержании. Согласно автору методички, относительная металлоемкость – это частное от деления веса станка на мощность его двигателя (тонн на киловатт). Разделили, например, 5 тонн на 2 кВт и получили 2,5 тонны на один кВт. Эти значения и представлены в таблице. Правильность и достоверность перечисленных фактов я снова оставлю на совести автора, да и, в конце концов, нам требуется обработать числа, а уж что это такое – не особо важно, хоть объём талии пчёлок. …И всё-таки математика немного шизофреническая наука :)

Решение:

ну, с пунктом а) справится даже неподготовленный человек. Очевидно, что для нахождения выборочной средней нужно просуммировать все значения и разделить полученный результат на объём выборки:

т/кВт (не забываем указать размерность!)

Эти и другие вычисления лучше проводить в Экселе, и чуть ниже будет ролик о том, как быстро выполнить все пункты задания. Ибо на калькуляторе щёлкать 30 слагаемых муторно (хотя, вариант вполне рабочий).

6.2.1. Равноинтервальная группировка

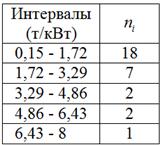
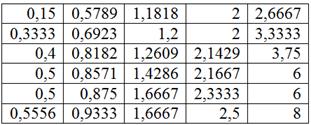
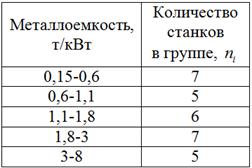
б) Выполним структурную равноинтервальную группировку. Пугаться не нужно, это задание уже было – нам нужно построить обычный интервальный вариационный ряд
с равными интервалами, и я кратко повторю алгоритм.

В условии ничего не сказано о количестве интервалов, и поэтому для определения их оптимального количества используем формулу Стерджеса:
интервалов (результат округляем влево).

Найдём минимальное и максимальное значения и вычислим размах вариации: т/кВт. Таким образом, длина частичного интервала составит: т/кВт. Теперь «нарезаем» интервалы и подсчитываем количество станков в каждом из них:

Контроль: , что и требовалось проверить.

И уже сейчас мы видим, что построенный вариационный ряд не слишком хорош – по той причине, что в трёх последних интервалах слишком мало станков, и считать по ним средние значения и другие показатели не вполне корректно. Во избежание этого недостатка используют разные методы, в частности, другой метод группировки:

6.2.2. Равнонаполненная группировка

в) Это разбиение совокупности на группы с одинаковым (или примерно одинаковым)количеством объектов, станков в данном случае. Но интервалы здесь получатся разной длины.

Отсортируем числа по возрастанию и выделим 5 групп по станков в каждой:

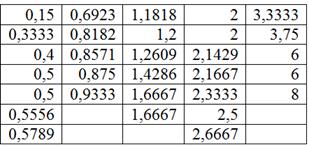
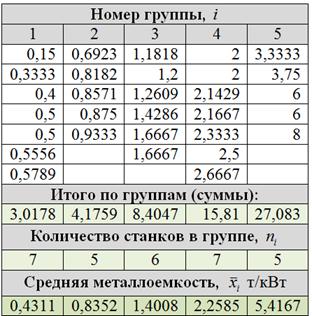
Формально всё выглядит тип-топ (и можно оставить так), но некоторые значения логичнее перенести в соседние группы. Так, значение 0,5789 (верхняя строка) явно ближе к 1-й группе, а значение 2,6667 – к предпоследней группе; туда их и перенесём:

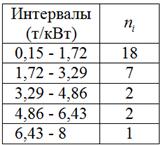
г) Очевидно, что равнонаполненная группировка более удачна, с ней и работаем. По каждой группе подсчитаем сумму, объём (количество станков) и выборочную среднюю – как результат деления суммы на соответствующий объём. Вычисления сведём в групповую таблицу:

И на всякий пожарный пример расчёта первой групповой средней:
т/кВт;
Да, кстати, не забываем предварительно проконтролировать объём выборки:
, ч.т.п.

д) Построим интервальный вариационный ряд по равнонаполненной группировке. Границы интервалов можно брать как средние арифметические «стыковых» значений, например: (граница между 1-м и 2-м интервалом). Но вполне допустимо (и даже лучше) разметить интервалы «на глазок», выбирая удобные «круглые» значения:

Полученный интервальный ряд имеет разную длину интервалов, но для него точно так же можно построить гистограмму, эмпирическую функцию распределения, а также рассчитать типовые характеристики. Правда, с модой проблема будет и для её нахождения таки лучше использовать равноинтервальную группировку (пункт б).

Теперь смотрим ролик по быстрому и эффективному выполнению расчётов.

Выражаясь научно, мы выполнили статистическую сводку.

Статистическая сводка – это комплекс действий по обработке статистических данных с целью получения обобщающих показателей и анализа стат. совокупности.

Причём, в пункте а) была простая статическая сводка (подсчёт общих показателей), которая переросла в сводку сложную, включающую в себя группировку данных, расчёт групповых характеристик и сведение результатов в групповую таблицу.
Но это ещё не всё:

е) Сделаем краткие выводы.

Я не случайно выделил данный пункт. Довольно часто в заданиях по статистике требуется сделать выводы – в них нужно отразить основные результаты выполненных действий и особенности исследуемой совокупности. Собственно, это и есть цель статистического исследования – сделать выводы.

И за нами дело не станет. Сказать здесь можно следующее. В результате исследования рассчитана средняя металлоёмкость т/кВт по выборке и средние значения по группам равнонаполненной (наиболее удачной) группировки. Большинство станков (18 шт. в первых трёх группах) имеют показатель металлоёмкости меньший, чем средняя металлоёмкость по выборке. Пять станков (группа 5) обладают значительно бОльшей металлоёмкостью, чем остальные, и причины этого требуют отдельного анализа (возможно, станки морально устарели).

Несколько строчек вполне достаточно, даже многовато получилось. Но это на пользу – грамотный аналитик или чиновник должен мастерски уметь «лить воду» J. …Вот видите, какой полезный курс….

Следующее задание для самостоятельного решения:

Пример 39

По результатам выборочного исследования 50 предприятий получены данные об их квартальной прибыли (числа в экселевском файле), млн. руб. Требуется:
1) вычислить среднюю прибыль;
2) провести равнонаполненную группировку и вычислить групповые средние;
3) построить соответствующий вариационный ряд;
4) сделать выводы.

Вообще, здесь удобно разбить выборку на 5 интервалов (и такой вариант вполне себе неплох), но от греха подальше лучше использовать формулу Стерджеса, что я и сделал в образце решения, который, как обычно, находится в конце книги. Ваш вариант решения может немного отличаться от моей версии. И выводы, разумеется, тоже.

Теперь вернёмся к пункту «бэ» Примера 38, где была выполнена не слишком удачная равноинтервальная группировка, скопирую табличку сверху:

Как вы помните, от «куцых» последних интервалов мы избавились, выполнив равнонаполненную группировку. Но есть и другой метод «лечения», который называется

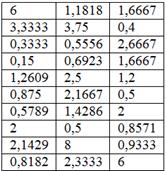
6.3. Перегруппировка

6.1. Группировка данных и её виды

| Оглавление |