Ваш репетитор, справочник и друг!

Математическая статистика – краткий курс для начинающих

3.1.4. Как вычислить среднюю, моду и медиану интервального ряда?

Начнём опять с ситуации, когда нам даны первичные статические данные:

Пример 10

По результатам выборочного исследования цен на ботинки в магазинах города получены следующие данные (ден. ед.):

– это в точности числа из Примера 6. Но теперь нам нужно найти среднюю, моду и медиану.

Решение: чтобы найти среднюю по первичным данным, нужно просуммировать все варианты и разделить полученный результат на объём совокупности:
ден. ед.

Эти подсчёты, кстати, займут не так много времени и при использовании оффлайн калькулятора. Но если есть Эксель, то, конечно, забиваем в любую свободную ячейку:
=СУММ(, выделяем мышкой все числа, закрываем скобку ), ставим знак деления /, вводим число 30 и жмём Enter. Готово.

Что касается моды, то её оценка по исходным данным, становится непригодна. Хоть мы и видим среди чисел одинаковые, но среди них запросто может найтись так 5-6-7 вариант с одинаковой максимальной частотой, например, частотой 2. Поэтому модальное значение рассчитывается по сформированному интервальному ряду (см. ниже).

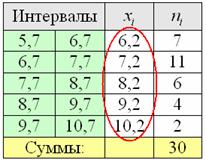
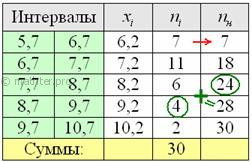
Чего не скажешь о медиане: забиваем в Эксель =МЕДИАНА(, выделяем мышью все числа, закрываем скобку ) и жмём Enter: . Причём, здесь даже ничего не нужно сортировать.

Но в Примере 6 я проводил сортировку совокупности по возрастанию (вспоминаем и сортируем), и это хорошая возможность повторить формальный алгоритм отыскания медианы.

Делим объём выборки пополам:
, и поскольку она состоит из чётного количества вариант, то медиана равна среднему арифметическому 15-й и 16-й варианты упорядоченного (!) вариационного ряда:
ден. ед.

Ситуация вторая. Когда даны не первичные данные, а готовый интервальный ряд (что в учебных задачах бывает чаще).

Продолжаем анализировать этот же пример с ботинками, где по исходным данным был составлен ИВР. Для вычисления средней потребуются середины интервалов:

– чтобы воспользоваться знакомой формулой дискретного случая:

– и это отличный результат! Расхождение с более точным значением (), вычисленным по первичным данным, составило всего 0,04!

Здесь мы использовали упомянутый ранее приём – приблизили интервальный ряд дискретным, и это приближение оказалось весьма эффективным. Впрочем, с современными программами не составляет особого труда вычислить точное значение даже по очень большому массиву первичных данных. Если они нам известны ;)

С другими центральными показателями всё занятнее.

Чтобы найти моду, нужно найти модальный интервал (с максимальной частотой) – в нашей задаче это интервал с частотой 11, и воспользоваться следующей страшненькой формулой:

, где:

– нижняя граница модального интервала;
– длина модального интервала;
– частота модального интервала;
– частота предыдущего интервала;
– частота следующего интервала.

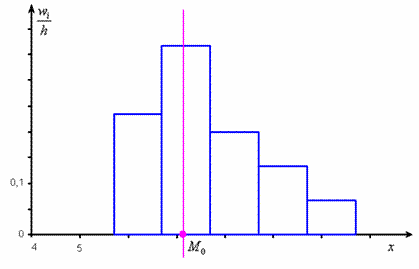
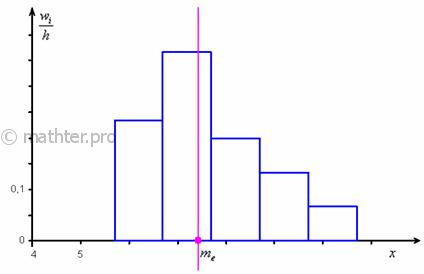
Таким образом:
ден. ед. – как видите, «модная» цена на ботинки заметно отличается от среднего арифметического значения .

Не вдаваясь в геометрию формулы, просто приведу гистограмму относительных частот и отмечу :

откуда хорошо видно, что мода смещена относительно центра модального интервала в сторону левого интервала с бОльшей частотой. По той причине, что дешёвых ботинок больше. И, возможно, они тоже вполне себе модные.

Справочно остановлюсь на редких случаях:
– если модальный интервал крайний, то либо ;
– если обнаружатся два смежных модальных интервала, например, и , то рассматриваем модальный интервал , при этом близлежащие интервалы (слева и справа) по возможности тоже укрупняем в два раза;
– если между модальными интервалами есть расстояние, то применяем формулу к каждому интервалу, получая тем самым две или бОльшее количество мод.

Вот такой вот депеш мод :)

И медиана. Она рассчитывается чуть по менее страшной формуле. Для её применения нужно найти медианный интервал – это интервал, содержащий варианту (либо 2 варианты), которая делит вариационный ряд на две равные части.

Выше я рассказал, как определить медиану, ориентируясь на относительные накопленные частоты , здесь же сподручнее рассчитать «обычные» накопленные частоты . Вычислительный алгоритм такой же – первое значение сносим слева (красная стрелка), а каждое следующее получается как сумма предыдущего с текущей частотой из левого столбца (зелёные обозначения в качестве примера):

Всем понятен смысл чисел в правом столбце? – это количество вариант, которые успели «накопится» на всех «пройденных» интервалах, включая текущий.
Поскольку у нас чётное количество вариант (30 штук), то медианным будет тот интервал, который содержит -ю и 16-ю варианту. И ориентируясь по накопленным частотам, легко прийти к выводу, что эти варианты содержатся в интервале .

Формула медианы:

, где:

– объём статистической совокупности;
– нижняя граница медианного интервала;
– длина медианного интервала;
– частота медианного интервала;
– накопленная частота предыдущего интервала.

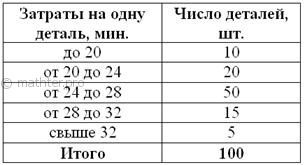
Таким образом:
ден. ед. – заметим, что медианное значение, в отличие от моды, оказалось смещено правее, т.к. по правую руку находится значительное количество вариант:

Справочно особые случаи:
– если медианным является крайний левый интервал, то ;
– если вариационный ряд содержит чётное количество вариант и две средние варианты попали в разные интервалы, то объединяем эти интервалы, и по возможности удваиваем предыдущий интервал.

Ответ: ден. ед.

По сравнению с предыдущей задачей , центральные показатели оказались заметно отличны друг от друга. Это говорит об асимметрии («скошенности») распределения цен, что хорошо видно по гистограмме и совершенно логично – ботинок низкого и среднего ценового сегмента много, а премиального – мало.

Задание для тренировки:

Пример 11

Для изучения затрат времени на изготовление одной детали рабочими завода проведена выборка, в результате которой получено следующее статистическое распределение:

…да, тот самый завод Петровского :) Найти среднюю, моду и медиану.

Решаем эту задачу в Экселе – все числа и инструкции уже там. Если нет Экселя, считаем на калькуляторе, что в данном случае может оказаться даже удобнее. Образец решения, как обычно, в конце книги. Это, кстати, уже каноничная «интервальная» задача, в которой исследуется непрерывная величина – время.

Что ещё можно сказать по теме?

Несмотря на разнообразия рассмотренных показателей, их всё равно бывает не достаточно. Существуют крайне неоднородные совокупности, у которых варианты «кучкуются» во многих местах, и по этой причине средняя, мода и медиана плохо характеризуют положение дел.

В таких случаях вариационный ряд дробят с помощью квартилей, децилей, а в упоротых специализированных исследованиях – и с помощью перцентилей.

Квартили упорядоченного вариационного ряда – это варианты , которые делят его на 4 равные (по количеству вариант) части. Из чего автоматически следует, что 2-я квартиль – есть в точности медиана: .

В тяжёлых случаях проводится разбиение на 10 частей – децилями – это варианты, который делят упорядоченный вариационный ряд на 10 равных (по количеству вариант) частей.

И в очень тяжелых случаях в ход пускается 99 перцентилей .

После разбиения вариационного ряда каждый участок исследуется по отдельности – рассчитываются локальные средние и другие показатели.

В учебном курсе квартили, децили, перцентили встречаются редко, и посему я оставляю этот материал (их нахождение) для самостоятельного изучения.

Ну а сейчас мы переходим к изучению второй группы статистических показателей:

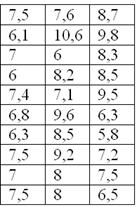
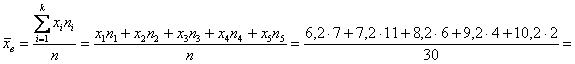
3.2. Показатели вариации

3.1.3. Медиана

| Оглавление |