Ваш репетитор, справочник и друг!

Математическая статистика – краткий курс для начинающих

3.1.3. Медиана

Медиана вариационного ряда* – это значение, которая делит его на две равные части (по количеству вариант).

* не важно, дискретного или интервального, генеральной совокупности или выборочной.

Медиану можно отыскать несколькими способами. Если даны первичные данные, то сортируем их по возрастанию либо убыванию и находим середину ранжированного ряда: . Почему именно 13-я варианта? Потому что перед ней находится 12 чисел и после неё тоже 12 чисел, таким образом, значение разделило ряд на две равные части, а значит, является медианой. Этот номер можно найти аналитически:

– если совокупность содержит нечётное количество вариант (наш случай), то делим её объём пополам: и округляем полученное значение в бОльшую сторону: 13 – получая тем самым номер искомой варианты;

– если совокупность содержит чётное количество вариант, например 20, то делаем то же самое: и медианное значение рассчитываем как среднее арифметическое 10-й и следующей варианты: .
Подчёркиваю, что изложенная выше инструкция работает для упорядоченного (по возрастанию либо убыванию) ряда. Но есть и более быстрый путь, где ничего не нужно сортировать. Это использование стандартной функции Экселя:

– забиваем в любую свободную ячейку =МЕДИАНА(, выделяем мышью все варианты, закрываем скобку ) и жмём Enter. Попробуйте самостоятельно. Этот способ удобен, когда вам дано много чисел.

Следует отметить, что в Экселе существуют и отдельные функции для вычисления средней (=СРЗНАЧ), моды (=МОДА) и ещё много чего, но я против использования этих функций в учебном курсе, за исключением случаев, где это действительно целесообразно. …Почему против? Потому что они не помогают понять суть показателей. Так, среднюю гораздо вразумительнее рассчитывать следующим образом:

=СУММ(выделяем мышью диапазон) / объем совокупности. Вычисления рекомендую опробовать лично (ссылка выше).

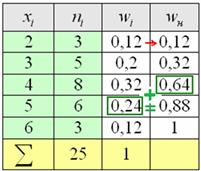
Ситуация вторая. Когда составлен либо изначально дан готовый дискретный ряд. Тут можно поступить «по любительски» – начать отсчитывать примерно равное количество вариант по краям ряда:

после чего мысленно либо на черновике их отбрасывать, в данном случае отбросим по 8 штук сверху и снизу:

откуда становится ясно, что медианное значение:

Или в более солидном стиле, находим относительные накопленные частоты:

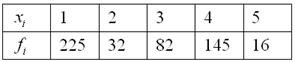
и ту варианту, у которой «перевалила» за отметку 0,5 (50% упорядоченной совокупности). Для варианты успело накопиться (32% совокупности), а вот для – уже (64%). Таким образом, отметка в 50% пройдена именно здесь, и, стало быть, .

Запишем красивый ответ:

И тут возникает следующий закономерный вопрос: а зачем вообще нужна мода с медианой? – ведь есть средняя. А дело в том, что в ряде случаев среднее значение неудовлетворительно характеризует центральную тенденцию совокупности:

Пример 9

Известны результаты продаж пиджаков в универмаге города:

где – количество пуговиц на пиджаке, – число продаж.

Обратите внимание, что в условии задачи ничего не сказано о том, генеральная ли это совокупность или выборочная, и в подобной ситуации я не рекомендую ничего додумывать – среднюю просто обозначаем через , без подстрочного индекса.

Задание: вычислить среднюю. В экселевском файле уже забиты исходные данные и приведена краткая инструкция. Если под пальцами нет Экселя, считаем на калькуляторе. Ну а если вам не нравятся пиджаки, то представьте какие-нибудь шляпки с цветочками:)

….Есть? Какие мысли на счёт полученного значения ? …С такой статистикой магазин разорится.

Ещё хуже в этом смысле ситуация с медианой, продолжаем решать задачу в Экселе либо в тетради. Особо зоркие читатели, медиану углядят устно.

И, конечно, важнейший показатель здесь мода: . Потому что такая мода :) Более того, в прикладных исследованиях рассматривают несколько модальных значений, в частности, ещё одной модой можно считать варианту . Но это уже «попсовая» статистика, которую я не буду развивать в настоящем курсе.

Теперь надеваем пиджаки / шляпы и возвращаемся на фабрику, где бухгалтер Петрова вычислила генеральную среднюю заработную плату рабочих: денежных единиц. Здесь мы плавно переходим к интервальному ряду, который целесообразно составлять для «денежных» показателей.

Что будет, если к совокупности добавить руководящий персонал и директора Петрова? Средняя зарплата немного увеличится: , и это уже будет несколько искажённая картина.

А вот если сюда добавить олигарха Петровского, то полученная средняя вообще вызовет широкое возмущение общественности.

Поэтому если в статистической совокупности есть «аномальные» отклонения в ту или иную сторону, то в качестве оценки центрального значения как нельзя лучше подходит медиана, которая в нашем условном примере будет равна, скажем, . Ниже этой планки зарабатывает ровно половина сотрудников фабрики и выше – другая половина, включая Петрова и Петровского. …Главное только, чтобы они наняли правильного статистика :)

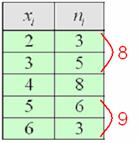
3.1.4. Как вычислить среднюю, моду и медиану интервального ряда?

3.1.2. Мода

| Оглавление |