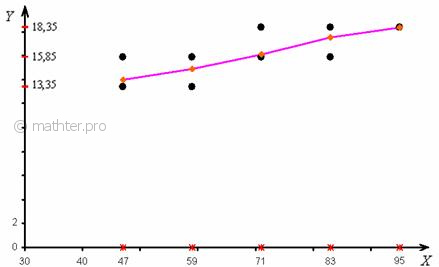
7.2. Эмпирические линии регрессии

По каждой группе признака-фактора (5 групп) рассчитаем средние значения признака-результата, результаты удобно свести в дополнительную строку таблицы:

Так, при выпуске млн. средняя прибыль составляет:
млн. руб.
и давайте ещё в качестве закрепляющего примера приведу расчёт для :
млн. руб.

Эмпирическая линия регрессии к (именно так!) – это ломаная, соединяющая точки :

Построенная ломаная проходит максимально близко к точкам корреляционного поля, при этом учитываются весомость частот , на основе которых были вычислены значения (см. вычисления перед чертежом).

Эмпирическая линия регрессии используется не только для наглядного изображения корреляционной зависимости, но и для интерполяции промежуточных значений…, сейчас объясню…. Рассматривая различные промежуточные значения выпуска продукции («иксы», отличные от ) с помощью ломаной мы можем достаточно точно оценить соответствующие средние значения прибыли («игреки средние»).

Но это ещё не всё. Встречаются ситуации, где признаки взаимно влияют друг на друга. Приведу философский пример, адаптированный к современным реалиям:)

– количество произведённых куриц на птицефабрике;
– количество произведённых яиц.

Совершенно понятно, что здесь, как признак влияет на , так и наоборот, и поэтому можно рассмотреть вторую корреляционную зависимость – «икса» от игрека. А также построить вторую эмпирическую линию регрессии.

Эмпирическая линия регрессии к (именно так!) – это ломаная, соединяющая точки , где – средние значения признака для различных значений (комбинационной таблицы) признака .

И в качестве тренировки

Задание

По данным вышеприведённого примера (30 предприятий) построить эмпирическую линию регрессии к .

Не ленимся! Формулы будут «зеркальными» и вычисления легко провести на обычном калькуляторе. Решение и чертёж в конце книги. Чуть позже я научу вас строить корреляционное поле в Экселе.

Наверное, вы заметили, что звенья ломаных расположились почти по прямой, и ещё более ярко эта тенденция прослеживается на диаграмме рассеяния, где точки «выстроились» примерно вдоль прямой линии.

В этой связи возникает заманчивая идея: а нельзя ли приблизить эмпирические точки линейной функцией?

Можно! (с)

Более того, во многих случаях это будет удачным решением! А, главное, технически простЫм.

Следующий параграф планировалась более 10 лет назад и вот, наконец, я здесь…. И вы здесь! И это замечательно! Даже не то слово. Это корреляционно:

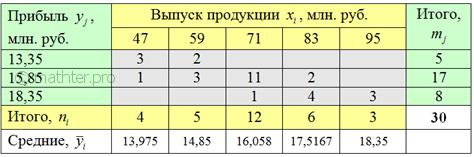
7.3. Модель пАрной линейной регрессиих

7.1. Графическое изображение эмпирических данных

| Оглавление |