7.3. Модель пАрной линейной регрессии

…И в этот момент я благоговейно улыбаюсь – как здОрово, что все мы здесь сегодня собрались:

Пример 45

Имеются выборочные данные по студентам: – количество прогулов за некоторый период времени и – суммарная успеваемость за этот период:

Сразу обращаю внимание, что в условии приведены несгруппированные данные. Помимо этого варианта, есть задачи, где изначально дана комбинационная таблица, и их мы тоже разберём. Сначала одно, затем другое.

Требуется:
– высказать предположение о наличии и характере зависимости признака-результата от признака-фактора ;
– построить диаграмму рассеяния и сделать вывод о форме зависимости;
– найти уравнение линейной регрессии на , выполнить чертёж;
– вычислить линейный коэффициент корреляции, сделать вывод;
– вычислить коэффициент детерминации, сделать вывод,

Решение: очевидно, что чем больше студент прогуливает, тем более вероятно, что у него плохая успеваемость. Но всегда ли это так? Нет, не всегда. Успеваемость зависит от многих факторов. Один студент может посещать все пары, но все равно учиться посредственно, а другой – учиться неплохо даже при большом количестве прогулов (не рекомендация! J – за всю жизнь я встретил двух-трёх человек с такими способностями). Однако общая тенденция состоит в том, что с увеличением количества прогулов средняя успеваемость студентов будет падать.

Таким образом, предполагаем наличие обратной корреляционной зависимости успеваемости от количества прогулов . Гипотезу проще всего проверить графически, построим диаграмму рассеяния:

Обратите, кстати, внимание как раз на тот момент, что при одном и том же количестве прогулов (15) двое студентов имеют существенно разные результаты.
По диаграмме рассеяния хорошо видно, что с увеличением числа прогулов успеваемость преимущественно падает, что подтверждает наличие обратной корреляционной зависимости успеваемости от количества прогулов. Более того, почти все точки «выстроились» примерно вдоль прямой, что даёт основание предположить, что данная зависимость близкА к линейной.

И здесь я анонсирую дальнейшие действия: нам предстоит найти уравнение прямой, ТАКОЙ, которая проходит максимально близко к эмпирическим точкам, а также оценить тесноту (силу) корреляционной линейной зависимости – насколько близко расположены точки к построенной прямой.

Технически существует два пути решения:

– сначала найти уравнение прямой и затем оценить тесноту зависимости;

– сначала найти тесноту и затем составить уравнение.

В практически задачах чаще встречается второй вариант, но я начну с первого, он более последователен. Построим:

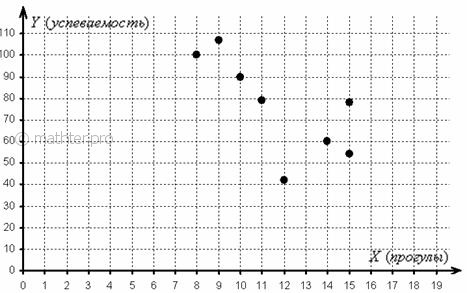
7.3.1. Уравнение линейной регрессии Y на X

7.2. Эмпирические линии регрессии

| Оглавление |