|
Ваш репетитор, справочник и друг!
|
7.3.1. Уравнение линейной регрессии Y на XЭто и есть та самая оптимальная прямая Коэффициенты «а» и «бэ» функции
Сократим оба уравнения на 2, всё попроще будет: Систему выгоднее решить по формулам
Крамера:
И проверка forever, подставим полученные значения Таким образом, искомое уравнение регрессии: и на самом деле «игрек» правильнее записать с чертой:
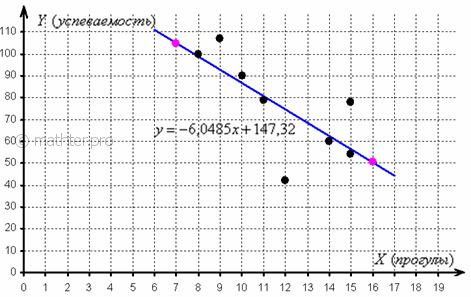
Полученное уравнение показывает, что с увеличением количества прогулов («икс») на 1 единицу суммарная успеваемость падает в среднем на 6,0485 – примерно на 6 баллов. Об этом нам рассказал коэффициент «а». И ещё раз обращаю внимание на тот факт, что найденная функция возвращает нам средние или среднеожидаемые значения «игрек» для различных значений «икс». А почему это регрессия именно « Линию регрессии изобразим на том же чертеже, вместе с диаграммой рассеяния. Для того чтобы построить прямую,
достаточно знать две точки, выберем пару удобных значений «икс» и вычислим соответствующие «игреки»: Говорят, что уравнение регрессии аппроксимирует (приближает) эмпирические данные (точки), и с помощью
него можно интерполировать (оценивать) неизвестные промежуточные значения, так при количестве прогулов И, конечно, осуществимо прогнозирование, так при Второй вопрос касается тесноты зависимости. Очевидно, что чем ближе расположены эмпирические
точки к прямой, тем теснее линейная корреляционная зависимость – тем уравнение регрессии достовернее отражает ситуацию, и тем
качественнее полученная модель. И наоборот, если многие точки разбросаны вдали от прямой, то признак
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Математическая статистика – краткий курс для начинающих
Математическая статистика – краткий курс для начинающих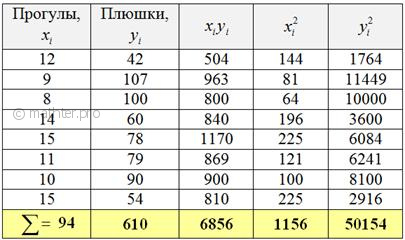
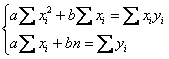 , в нашей
задаче:
, в нашей
задаче:
 7.3.2. Линейный коэффициент корреляции
7.3.2. Линейный коэффициент корреляции 7.3. Модель пАрной линейной регрессиих
7.3. Модель пАрной линейной регрессиих