7.3.2. Линейный коэффициент корреляции
Этот коэффициент как раз и оценивает тесноту линейной корреляционной зависимости и более того, указывает её
направление (прямая или обратная). Его полное название: выборочный линейный коэффициент пАрной
корреляции Пирсона :)
– выборочный – потому что мы рассматриваем выборочную
совокупность;
– линейный – потому что он оценивает тесноту линейной корреляционной зависимости;
– пАрной – потому что у нас два признака (бывает хуже);
– и «Пирсона» – в честь английского статистика Карла Пирсона, это он автор понятия «корреляция».
А в зависимости от фантазии автора задачи вам может встретиться любая комбинация прокомментированных слов. Теперь нас не
застанешь врасплох, Карл.
Линейный коэффициент корреляции вычислим по формуле:
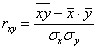 , где: , где: 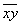 – среднее значение произведения признаков, – среднее значение произведения признаков, 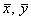 – средние значения признаков и – средние значения признаков и 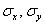 – стандартные отклонения признаков. Числитель формулы имеет особый смысл, о
котором я расскажу позже, когда мы будем разбирать второй способ решения. – стандартные отклонения признаков. Числитель формулы имеет особый смысл, о
котором я расскажу позже, когда мы будем разбирать второй способ решения.
Осталось разгрести всё это добро :) Впрочем, все нужные суммы уже рассчитаны в таблице выше. Вычислим средние
значения:
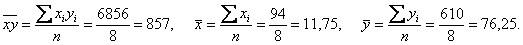
Стандартные отклонения найдём как корни из соответствующих дисперсий, вычисленных по формуле:
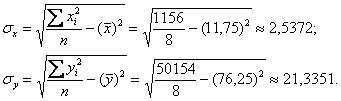
Таким образом, коэффициент корреляции:
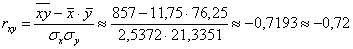
И расшифровка: коэффициент корреляции может изменяться в пределах 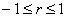 и чем он ближе по модулю к единице, тем теснее линейная корреляционная
зависимость – тем ближе расположены точки к прямой, тем качественнее и достовернее линейная модель. Если и чем он ближе по модулю к единице, тем теснее линейная корреляционная
зависимость – тем ближе расположены точки к прямой, тем качественнее и достовернее линейная модель. Если 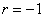 или или 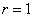 , то речь идёт о строгой линейной зависимости, при
которой все эмпирические точки окажутся на построенной прямой. Наоборот, чем ближе , то речь идёт о строгой линейной зависимости, при
которой все эмпирические точки окажутся на построенной прямой. Наоборот, чем ближе 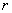 к нулю, тем точки рассеяны дальше, тем линейная зависимость
выражена меньше. Однако в последнем случае зависимость всё равно может быть! – например, нелинейной или какой-нибудь
более загадочной. Но до этого мы ещё дойдём. А у кого не хватит сил, донесём :) к нулю, тем точки рассеяны дальше, тем линейная зависимость
выражена меньше. Однако в последнем случае зависимость всё равно может быть! – например, нелинейной или какой-нибудь
более загадочной. Но до этого мы ещё дойдём. А у кого не хватит сил, донесём :)
Для оценки тесноты связи используют так называемую шкалу Чеддока, в разных источниках она может иметь немного
разные градации, например, такую:
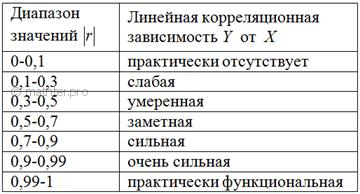
при этом если 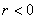 , то
корреляционная связь обратная, а если , то
корреляционная связь обратная, а если 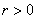 , то прямая. , то прямая.
У нас 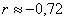 , таким
образом, существует сильная обратная корреляционная зависимость , таким
образом, существует сильная обратная корреляционная зависимость 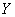 – суммарной успеваемости от – суммарной успеваемости от 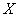 – количества прогулов. Немудрено. – количества прогулов. Немудрено.
 7.3.3. Коэффициент детерминации 7.3.3. Коэффициент детерминации
 7.3.1. Уравнение линейной регрессии Y на X 7.3.1. Уравнение линейной регрессии Y на X
| Оглавление |
|

 Математическая статистика – краткий курс для начинающих
Математическая статистика – краткий курс для начинающих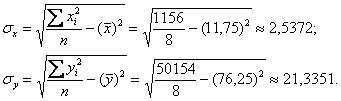

 7.3.3. Коэффициент детерминации
7.3.3. Коэффициент детерминации 7.3.1. Уравнение линейной регрессии Y на X
7.3.1. Уравнение линейной регрессии Y на X