|
Ваш репетитор, справочник и друг!
|
3.2.5. Вычисление дисперсии по формулеЭта формула выводится непосредственно из определения:
ОСМЫСЛЕННО повторяем ВСЛУХ и вникаем! … Карл украл у Клары кораллы, а Клара украла у Карла кларнет! Если что-то не очень понятно, то сейчас всё станет на свои места: Для несгруппированных вариант Для генеральной дисперсии И начнём мы со знакомой подопытной задачи: Пример 15 В результате 10 независимых измерений получены следующие данные: В Примере 13 мы нашли дисперсию по определению: Решение: используем формулу Ответ: Теперь случай сформированного вариационного ряда. В Примере 14 мы потренировались на дискретном ряде, и сейчас очередь интервального: Пример 16 С целью изучения вкладов в Сбербанке города проведено выборочное исследование, в результате которого получены следующие
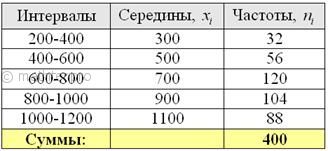
данные: Вычислить выборочную дисперсию и среднее квадратическое отклонение, оценить соответствующие показатели генеральной совокупности. Автор задачи заботливо подсчитал объем выборки поскольку длины внутренних интервалов составляют …Возможно, у вас возник вопрос, а как быть, если даны интервалы разной длины? В этом случае можно принять за «эталон» среднюю длину известных интервалов. Для расчёта числовых характеристик перейдём к дискретному вариационному ряду,
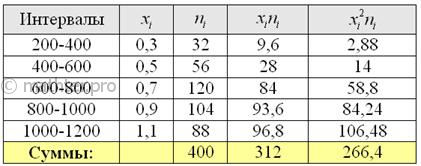
выбрав в качестве вариант Кроме того, варианты целесообразно уменьшить в 1000 раз, поскольку в ходе дальнейших вычислений будут получаться гигантские числа. С современной техникой, это, конечно, не проблема, но смотреться будет некрасиво. Сначала вычислим выборочную среднюю. Этот алгоритм уже обкатан: находим
произведения Примечание: далее для компактной записи я буду использовать просто значок Теперь дисперсия. Её никто не запрещает рассчитать по определению Итак, по формуле вычисления дисперсии, получаем: И, чтобы вернуться в размерность задачи, из дисперсии следует извлечь квадратный корень:
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Математическая статистика – краткий курс для начинающих
Математическая статистика – краткий курс для начинающих
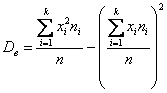 , где
, где 
 .
.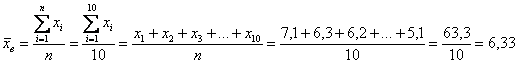 ,
, 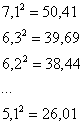
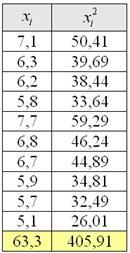
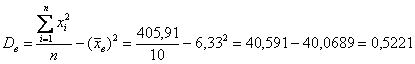 , что мы и хотели увидеть – результат,
естественно, совпал с полученным ранее по определению.
, что мы и хотели увидеть – результат,
естественно, совпал с полученным ранее по определению.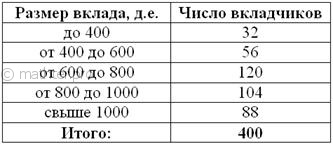
 3.2.6. Среднее квадратическое отклонение
3.2.6. Среднее квадратическое отклонение 3.2.4. Исправленная выборочная дисперсия
3.2.4. Исправленная выборочная дисперсия