|
Ваш репетитор, справочник и друг!
|
3.2.3. Генеральная и выборочная дисперсияДисперсия с латыни так и переводится – рассеяние. …Не сломать бы язык :) …так: выборочная дисперсия – это среднее арифметическое
квадратов отклонений всех вариант выборки от её средней: Ещё раз не спеша и ОСМЫСЛЕННО прочитайте определение и выполните Задание: сформулировать и записать (на бумагу!) определение генеральной дисперсии и соответствующие формулы. Свериться можно в конце книги. Вычислим дисперсию по данным Примера 13. Здесь вместо модулей нужно рассчитать квадраты отклонений: Заполняем табличку: Ответ: Разобранная только что задача часто встречается в лабораторных работах по физике (да и не только) – когда некоторая величина замеряется раз десять и затем рассчитывается среднее значение. А теперь представьте, что вся ваша группа выполняет лабу по физике, и каждый провёл по 10 испытаний в схожих условиях.
Очевидно, что у всех получились несколько разные выборочные значения Теперь пару ласковых об отклонениях. В чём их смысл? Всё просто: у кого эти показатели ниже, тот качественнее проводит
опыты (плавнее выполняет действия, точнее снимает показания с приборов, засекает время и т.п.). В идеале эти
отклонения равны нулю, но это только в идеале – сам эмпиризм ситуации порождает генеральное линейное отклонение В случае с полученными линейными отклонениями
Показатель
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Математическая статистика – краткий курс для начинающих
Математическая статистика – краткий курс для начинающих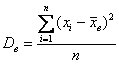 – для несгруппированных данных, и:
– для несгруппированных данных, и: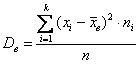 – для сформированного вариационного ряда,
где
– для сформированного вариационного ряда,
где 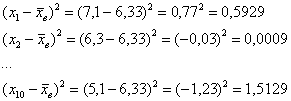
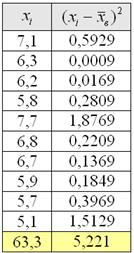
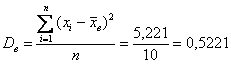 квадратных (!) единиц –
коль скоро, мы возводили в квадрат. И, чтобы вернуться в размерность задачи, из дисперсии следует извлечь квадратный корень.
Но мы не будем торопить события, лучше посмотрим,
квадратных (!) единиц –
коль скоро, мы возводили в квадрат. И, чтобы вернуться в размерность задачи, из дисперсии следует извлечь квадратный корень.
Но мы не будем торопить события, лучше посмотрим,  3.2.4. Исправленная выборочная дисперсия
3.2.4. Исправленная выборочная дисперсия 3.2.2. Среднее линейное отклонение
3.2.2. Среднее линейное отклонение