|
Ваш репетитор, справочник и друг!
|
3.2.2. Среднее линейное отклонение
Если же в нашем распоряжении есть сформированный дискретный либо интервальный вариационный ряд, то формула будет такой:
Напоминаю, что маленькая буква Пример 13 В результате 10 независимых измерений некоторой величины, выполненных с одинаковой точностью, полученные опытные данные,
которые представлены в таблице Требуется вычислить среднее линейное отклонение. Решение: очевидно, что перед нами первичные данные и выборочная совокупность (теоретически измерений
можно провести бесконечно много). На первом шаге вычислим выборочную
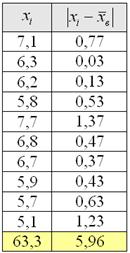
среднюю: Теперь находим модули отклонений от средней: Вычисления удобно проводить на калькуляторе или в Экселе (видео ниже), а результаты заносить в таблицу: На завершающем этапе рассчитываем сумму модулей: Ответ: Среднее линейное отклонение – это хорошо, но помимо него, для оценки рассеяния вариант относительно
средней существует более совершенный и распространённый подход. Он состоит в том, чтобы использовать не модули, а
возведение отклонений в квадрат: В результате получается:
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Математическая статистика – краткий курс для начинающих
Математическая статистика – краткий курс для начинающих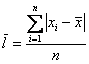 – есть среднее арифметическое
абсолютных отклонений всех значений статистической совокупности от средней. Это формула для
несгруппированных статистических данных.
– есть среднее арифметическое
абсолютных отклонений всех значений статистической совокупности от средней. Это формула для
несгруппированных статистических данных. 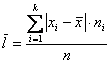 , где
, где 
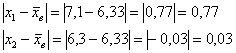
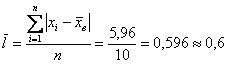 ед. – оно означает, что измеренные
значения
ед. – оно означает, что измеренные
значения  3.2.3. Генеральная и выборочная дисперсия
3.2.3. Генеральная и выборочная дисперсия 3.2.1. Размах вариации
3.2.1. Размах вариации