|
Ваш репетитор, справочник и друг!
|
3.2.4. Исправленная выборочная дисперсияи вот она уже является несмещённой оценкой генеральной дисперсии. Таким образом, каждый студент должен поправить свою дисперсию, в частности, для данных Примера 13: Следует отметить, что в больших выборках (от 30 вариант) этой поправкой можно пренебречь, так как при И иногда дисперсию лучше вовсе не поправлять. Так, в разобранном примере от нас требовалось просто вычислить выборочную
дисперсию и всё. Поэтому в ответе записываем Теперь случай, когда дан готовый вариационный ряд. У меня опять есть подходящая советская задача про телефонную станцию, но я скорректирую условие в соответствии с современными реалиями: Пример 14 В результате выборочного исследования звонков, статистик МТС получил следующие данные (за некоторый временной
промежуток): Решить данную задачу в Экселе (данные и гайд уже там) либо на бумаге с помощью калькулятора. Краткое решение и ответ в конце книги. Теперь вернёмся к технике вычисления дисперсии. Выше мы её рассчитывали по
определению: Расчёт дисперсии по определению прост и реально используется на практике, но существует ещё более простой и удобный способ –
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Математическая статистика – краткий курс для начинающих
Математическая статистика – краткий курс для начинающих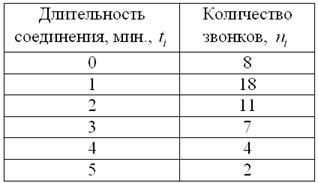
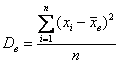 – для несгруппированных
данных и
– для несгруппированных
данных и 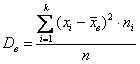 – для дискретного либо
интервального вариационного ряда. Это для
– для дискретного либо
интервального вариационного ряда. Это для  3.2.5. Вычисление дисперсии по формуле
3.2.5. Вычисление дисперсии по формуле 3.2.3. Генеральная и выборочная дисперсия
3.2.3. Генеральная и выборочная дисперсия