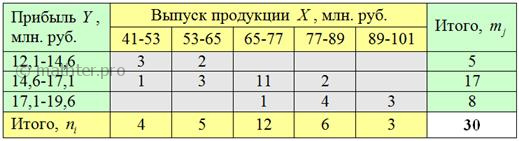
7.1. Графическое изображение эмпирических данных

Вернёмся к «избитому» ещё не до конца Примеру 42, где дано 30 предприятий с известными значениями выпуска продукции (признак-фактор ) и соответствующими значениями прибыли (признак-результат ). По первичным данным строится

7.1.1. Диаграмма рассеяния

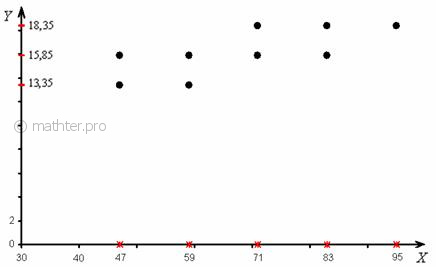
– это множество точек в декартовой системе координат, абсциссы которых соответствуют значениям признака-фактора , а ординаты – соответствующим значениям признака-результата . Вот наши 30 предприятий:

И тут не нужно быть экспертом, чтобы понять, что при увеличении выпуска продукции растут и прибыли предприятий.

Если зависимость обратная («чем больше, тем меньше»), то точки имеют тенденцию располагаться наоборот – от левого верхнего угла к правому нижнему. И такой пример будет позже.

Если точки распределены по диаграмме примерно равномерно (нет явной закономерности), то корреляционная зависимость слабА либо отсутствует.

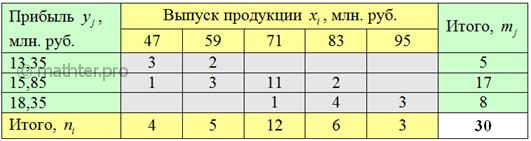
Минимальное количество точек должно равняться пяти-шести, в противном случае корреляционный анализ становится некорректным. А если точек много (30-50 и больше), то этот анализ усложняется и диаграмма «замусоривается». В таких случаях первичные данные подвергают группировке, как правило, комбинационной:

После чего комбинационную таблицу упрощают. А именно переходят от интервальных вариационных рядов («шапка» таблицы и левый столбец) к дискретным, выбрав в качестве вариант и середины соответствующих интервалов:

И, наконец, для сгруппированных данных строят

7.1.2. Корреляционное поле

– это множество точек с абсциссами и ординатами , которые соответствуют ненулевым значениям частот комбинационной таблицы:

Мысленно сопоставьте таблицу с картинкой! При этом сами частоты (числа в серых ячейках) на чертеже никак не отмечаются. И по внешнему виду корреляционного поля легко понять, что зависимость здесь прямая («чем больше, тем больше»).

Далее. Построенные чертежи наводят нас на светлую мысль, что эмпирические точки было бы удобно приблизить некоторой функцией, которая удачно характеризует зависимость. И здесь мы подошли к третьему слову заголовка главы – «регрессионного».

В статистическом смысле регрессия – это зависимость средних значений признака-результата от соответствующих значений признака-фактора. Термин «регрессия» появился исторически, и желающие могут найти эту историю в Сети. Если быть лаконичным, то полученные средние значения «игрек» регрессивно возвращают нас к первопричине – соответствующим исходным значениям «икс».

И дело за тем, чтобы найти функцию, которая для различных значений «икс» определяла бы нам средние значения «игрек». В случае несгруппированных данных это не самая простая задача, а вот для комбинационной группировки есть очевидное решение:

7.2. Эмпирические линии регрессии

7. Элементы корреляционно-регрессионного анализа

| Оглавление |