7.3.6. Уравнение линейной регрессии X на Y
– его можно составить (в том числе и для несгруппированных
данных) по формуле:
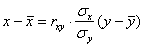 , после чего
свести к виду: , после чего
свести к виду:
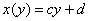 – полученное
уравнение позволяет нам узнать средние значения «икс», соответствующие различным значениям «игрек» – полученное
уравнение позволяет нам узнать средние значения «икс», соответствующие различным значениям «игрек»
Чисто формально эта регрессия всегда существует, так в рассмотренной задаче признак 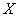 явно не зависит от явно не зависит от 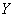 , но вот линейная корреляционная
зависимость есть! Причём, такой же тесноты. Из этого следуют важные факты, о которых мы поговорим в следующем параграфе.
Кроме того, существуют ситуации, где признаки взаимно влияют друг на друга, уже известный вам пример: , но вот линейная корреляционная
зависимость есть! Причём, такой же тесноты. Из этого следуют важные факты, о которых мы поговорим в следующем параграфе.
Кроме того, существуют ситуации, где признаки взаимно влияют друг на друга, уже известный вам пример:
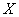 –
количество произведённых куриц на птицефабрике; –
количество произведённых куриц на птицефабрике;
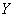 –
количество произведённых яиц. –
количество произведённых яиц.
Здесь в уравнении регрессии 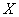 на на 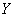 – самый что ни на есть здравый смысл. – самый что ни на есть здравый смысл.
График регрессии 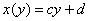 тоже можно изобразить на чертеже, и примечателен тот
факт, что он будет пересекать график «традиционной» регрессии тоже можно изобразить на чертеже, и примечателен тот
факт, что он будет пересекать график «традиционной» регрессии 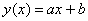 в точности в точке в точности в точке 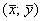 . .
Следующая задачка для самостоятельного решения:
Пример 48
Известны следующие данные:
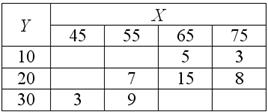
Найти линейный коэффициент корреляции и уравнение регрессии 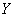 на на 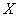 , а также , а также 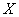 на на 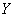 . Построить корреляционное поле, линии регрессии и
определить их точку пересечения. Вычислить . Построить корреляционное поле, линии регрессии и
определить их точку пересечения. Вычислить 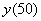 и и 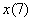 . По каждому пункту сделать выводы. . По каждому пункту сделать выводы.
Все числа уже в Экселе и вам остаётся выполнить вычисления, ничего страшного, если
получится не очень красиво, важнА тренировка.
Обратите внимание, что в этом примере ничего не сказано о признаках 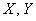 , но нам ничего и не нужно о них знать, ведь задачу можно
решить чисто формально – вне зависимости от того, где здесь признак-фактор, а где результат, и есть ли вообще
причинно-следственная связь между признаками. , но нам ничего и не нужно о них знать, ведь задачу можно
решить чисто формально – вне зависимости от того, где здесь признак-фактор, а где результат, и есть ли вообще
причинно-следственная связь между признаками.
 7.4. Корреляционная зависимость и причинно-следственная связь + итоги 7.4. Корреляционная зависимость и причинно-следственная связь + итоги
 7.3.5. Как решить задачу в случае комбинационной группировки 7.3.5. Как решить задачу в случае комбинационной группировки
| Оглавление |
|

 Математическая статистика – краткий курс для начинающих
Математическая статистика – краткий курс для начинающих
 7.4. Корреляционная зависимость и причинно-следственная связь + итоги
7.4. Корреляционная зависимость и причинно-следственная связь + итоги 7.3.5. Как решить задачу в случае комбинационной группировки
7.3.5. Как решить задачу в случае комбинационной группировки