7.3.5. Как решить задачу в случае комбинационной группировки
Это когда в условии дана комбинационная таблица:
Пример 47
Имеются выборочные данные по 40 предприятиям региона:
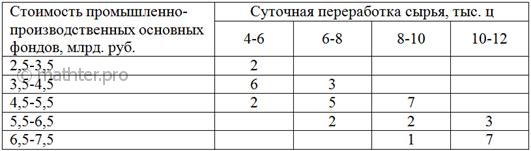
Требуется:
1) Определить признак-фактор 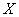 и признак-результат и признак-результат 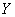 и высказать предположение о наличии и направлении зависимости и высказать предположение о наличии и направлении зависимости 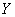 от от 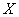 . Построить корреляционное поле и выдвинуть
гипотезу о возможной форме зависимости. . Построить корреляционное поле и выдвинуть
гипотезу о возможной форме зависимости.
2) Найти коэффициенты корреляции и детерминации, сделать выводы.
3) Найти уравнение регрессии 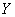 на на 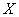 и изобразить соответствующую линию на чертеже.
Спрогнозировать среднюю суточную переработку сырья, когда стоимость основных фондов предприятий достигнет 9 млрд. руб. и изобразить соответствующую линию на чертеже.
Спрогнозировать среднюю суточную переработку сырья, когда стоимость основных фондов предприятий достигнет 9 млрд. руб.
Решение:
1) Определим признак-фактор и признак-результат. Очевидно,
что чем больше стоимость основных фондов, тем крупнее предприятие и тем больше сырья оно способно переработать. Однако это не
является непреложным правилом, ибо любое, самое крупное предприятие может неэффективно работать или даже простаивать. Тем не
менее, общая тенденция состоит в том, что при увеличении стоимости фондов предприятий их средняя суточная
переработка растёт. Такая зависимость называется… Правильно! Таким образом, предполагаем наличие прямой корреляционной зависимости суточной переработки сырья
(признак-результат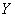 )
от стоимости основных фондов (признак-фактор )
от стоимости основных фондов (признак-фактор 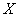 ) )
Частоты комбинационной таблицы располагаются преимущественно по диагонали – от левого верхнего до правого
нижнего угла, что подтверждает прямое направление зависимости («чем больше, тем больше»).
Теперь определим форму зависимости (линейная, квадратичная, экспоненциальная или какая-то другая).
Простейший способ – графический, построили корреляционное поле и посмотрели. Для этого
нужно немного модифицировать исходную таблицу, а именно перейти от интервальных
вариационных рядов (левый столбец и шапка таблицы) к дискретным, выбрав
в качестве вариант 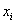 и и
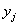 середины
соответствующих интервалов: середины
соответствующих интервалов:
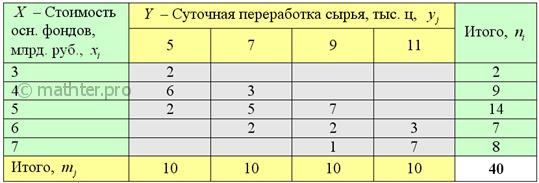
Заодно подсчитаем суммы частот по серым строкам 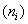 и суммы частот по серым столбцам и суммы частот по серым столбцам 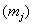 , не забыв убедиться в том, что итоговые суммы равны
объёму выборки: , не забыв убедиться в том, что итоговые суммы равны
объёму выборки:

Довольно часто значения 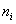 и и 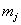 уже подсчитаны и приведены в условии, но так бывает не во всех
задачах, и поэтому я насыщаю решение всеми возможными действиями. уже подсчитаны и приведены в условии, но так бывает не во всех
задачах, и поэтому я насыщаю решение всеми возможными действиями.
Обратите внимание, что значения 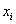 признака-фактора расположены по
вертикали в левом столбце, а значения признака-фактора расположены по
вертикали в левом столбце, а значения 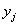 признака-результата – по
горизонтали в «шапке» таблицы. Именно такое расположение (а не наоборот) чаще всего встречается на практике, хотя оно
не сильно удобно, в частности для построения корреляционного поля: признака-результата – по
горизонтали в «шапке» таблицы. Именно такое расположение (а не наоборот) чаще всего встречается на практике, хотя оно
не сильно удобно, в частности для построения корреляционного поля:
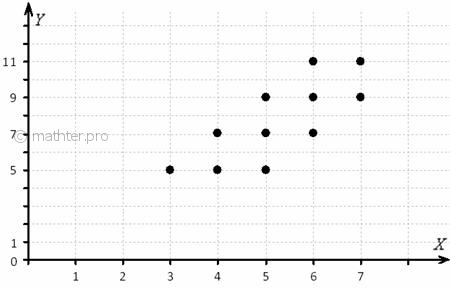
Ранее мы строили эмпирические линии регрессии – это простейший способ
изобразить форму корреляционной зависимости. Однако гораздо удобнее привлечь на помощь функции. Анализируя чертёж,
приходим к выводу, что эмпирические точки 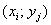 «выстроились» примерно по прямой, что позволяет предположить
наличие линейной корреляционной зависимости «выстроились» примерно по прямой, что позволяет предположить
наличие линейной корреляционной зависимости 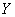 – суточной переработки сырья от – суточной переработки сырья от 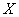 – стоимости основных фондов. – стоимости основных фондов.
Дальнейшие действия состоят в том, чтобы отыскать уравнение линейной
регрессии 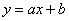 , график
которой проходит максимально близко к эмпирическим точкам (с учётом их «весов» – частот , график
которой проходит максимально близко к эмпирическим точкам (с учётом их «весов» – частот 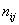 в серых полях комбинационной таблицы), а
также оценить тесноту линейной корреляционной зависимости – насколько близко расположены точки к построенной прямой.
Эта теснота оценивается с помощью линейного коэффициента корреляции, с него и
начнём: в серых полях комбинационной таблицы), а
также оценить тесноту линейной корреляционной зависимости – насколько близко расположены точки к построенной прямой.
Эта теснота оценивается с помощью линейного коэффициента корреляции, с него и
начнём:
2) Коэффициент корреляции вычислим по знакомой формуле 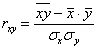 . .
Лично я привык в первую очередь находить средние 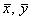 и стандартные отклонения и стандартные отклонения 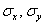 . Эти расчёты мы проводили неоднократно. . Эти расчёты мы проводили неоднократно.
Сначала разберёмся с признаком-фактором 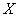 . Для этого из комбинационной таблицы (см. выше)
выпишем значения . Для этого из комбинационной таблицы (см. выше)
выпишем значения 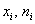 и
заполним расчётную таблицу: и
заполним расчётную таблицу:
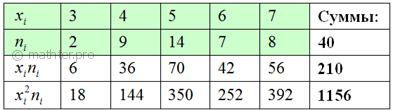
Вычислим среднее значение 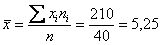 млрд. руб. и среднее квадратическое отклонение, как корень из
дисперсии, вычисленной по формуле: млрд. руб. и среднее квадратическое отклонение, как корень из
дисперсии, вычисленной по формуле:
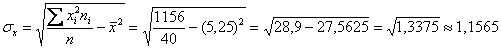
Аналогично, берём игрековые значения из комбинационной таблицы и заполняем расчетную таблицу для
признака-результата  : :
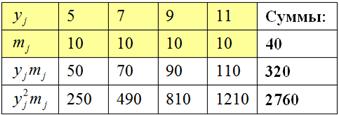
после чего рассчитываем нужные показатели:
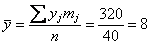 тыс. ц; тыс. ц;
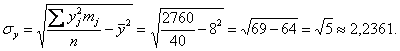
Теперь найдём среднее значение 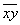 произведения признаков. Для этого вычислим все возможные
произведения произведения признаков. Для этого вычислим все возможные
произведения 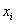 и и 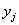 на соответствующие
ненулевые частоты на соответствующие
ненулевые частоты 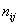 ,
наглядно распишу парочку штук: ,
наглядно распишу парочку штук:
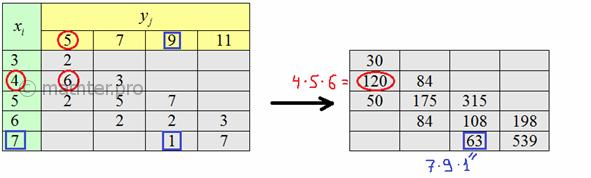
Вычислим сумму этих произведений:
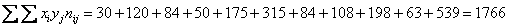
и искомую среднюю: 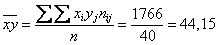 . .
И мы счастливы:
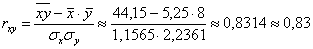 – в результате
получено положительное число и, согласно шкале Чеддока, существует
сильная прямая линейная корреляционная зависимость – в результате
получено положительное число и, согласно шкале Чеддока, существует
сильная прямая линейная корреляционная зависимость 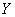 суточной переработки сырья от суточной переработки сырья от 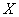 стоимости фондов. стоимости фондов.
Вычислим коэффициент детерминации:
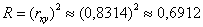 , таким образом,
в рамках построенной модели 69,12% вариации суточной переработки сырья обусловлено стоимостью основных
фондов. Остальные , таким образом,
в рамках построенной модели 69,12% вариации суточной переработки сырья обусловлено стоимостью основных
фондов. Остальные 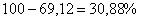 вариации обусловлено другими факторами. вариации обусловлено другими факторами.
3) Найдём уравнение 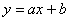 линейной регрессии линейной регрессии 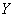 на на 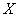 . Здесь можно использовать уже известные формулы . Здесь можно использовать уже известные формулы 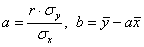 , но есть более академичный вариант. Искомое уравнение имеет
вид: , но есть более академичный вариант. Искомое уравнение имеет
вид:
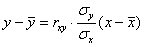 , в данной
задаче (вычисления приближённые): , в данной
задаче (вычисления приближённые):
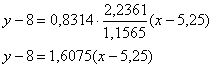
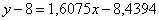 , примерно: , примерно:
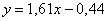
Полученное уравнение показывает, что при увеличении стоимости основных фондов на 1 млрд. руб. суточная переработка сырья
увеличивается в среднем на 1,61 тысяч центнеров (смысл коэффициента «а»). Напоминаю, что функция регрессии
возвращает нам среднеожидаемые значения «игрек».
Найдём пару удобных точек для построения графика:
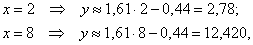
отметим их на чертеже (красный цвет) и аккуратно проведём линию регрессии на том же чертеже:
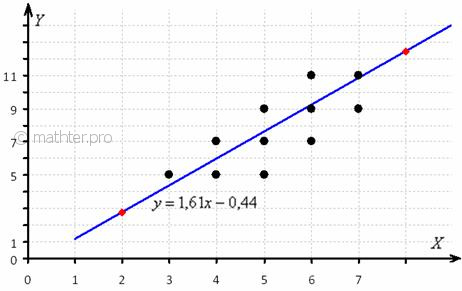
С помощью уравнения спрогнозируем среднюю суточную переработку сырья при стоимости основных фондов в 9 млрд.
руб.:
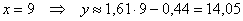 тыс. ц. тыс. ц.
Теперь видео о том, как быстро расправиться с этой
задачей:
Помимо рассмотренного, существует второе уравнение –
 7.3.6. Уравнение линейной регрессии X на Y 7.3.6. Уравнение линейной регрессии X на Y
 7.3.4. Второй способ решения 7.3.4. Второй способ решения
| Оглавление |
|

 Математическая статистика – краткий курс для начинающих
Математическая статистика – краткий курс для начинающих




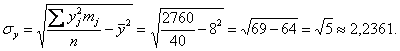

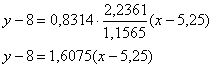

 7.3.6. Уравнение линейной регрессии X на Y
7.3.6. Уравнение линейной регрессии X на Y 7.3.4. Второй способ решения
7.3.4. Второй способ решения