7.3.4. Второй способ решения

Где мы сначала находим коэффициент корреляции, а затем уравнение регрессии.

Линейный коэффициент корреляции вычислим по формуле:
, где – стандартные отклонения признаков .

Член в числителе называют корреляционным моментом или коэффициентом ковариации (совместной вариации) признаков, он рассчитывается следующим образом: , где – объём статистической совокупности, а – средние значения признаков. Данный коэффициент показывает, насколько согласованно отклоняются пАрные значения от своих средних в ту или иную сторону. Формулу можно упростить, в результате чего получится ранее использованная версия, без подробных выкладок: . Но сейчас мы пойдём другим путём. Заполним расчётную таблицу:

В ходе заполнения таблицы сначала рассчитываем левые нижние суммы и средние значения признаков: и только потом заполняем оставшиеся столбцы таблицы. Кино будет!

Вычислим коэффициент ковариации:
.

Стандартные отклонения вычислим как квадратные корни из дисперсий:

Таким образом, коэффициент корреляции:

И если нам известны значения , то коэффициенты уравнения регрессии легко рассчитать по следующим формулам:

Таким образом, искомое уравнение:

Полученные результаты, естественно, совпали с результатами и выводами, сделанными ранее.

Теперь смотрим ролик о том, как это всё быстро подсчитать и построить.

Если под рукой нет Экселя, ничего страшного, разобранную задачу не так трудно решить в обычной клетчатой тетради.

Какой способ выбрать? Ориентируйтесь на свой учебный план и методичку. По умолчанию лучше использовать 2-й способ решения, он несколько короче, и, вероятно, потому и встречается чаще. Кстати, если вам нужно построить ТОЛЬКО уравнение регрессии, то уместен 1-й способ, ибо там мы находим это уравнение в первую очередь.

Следующая задача много-много лет назад была предложена курсантам местной школы милиции (тогда ещё милиции), и это чуть ли не первая задача по теме, которая встретилась в моей профессиональной карьере. Поэтому я безмерно рад предложить её вам сейчас:

Пример 46

В результате независимых опытов получены 7 пар чисел:

…да, числа могут быть и отрицательными.

По данным наблюдений вычислить линейный коэффициент корреляции и детерминации, сделать выводы. Найти параметры линейной регрессии на , пояснить их смысл. Изобразить диаграмму рассеяния и график регрессии. Вычислить и пояснить, что означают полученные результаты.

Все данные уже забиты в Эксель, и вам осталось аккуратно выполнить расчёты. В образце я решил задачу вторым, более распространённым способом. И, конечно же, выполните проверку первым путём.

Следует отметить, что в целях экономии места и времени я специально подобрал задачи с малым объёмом выборки. На практике обычно предлагают 10 или 20 пар чисел, реже 30, и максимальная выборка, которая мне встречалась в студенческих работах – 100. …Соврал немного, 80. Ну а минимальное значение, напоминаю, 5-6 пар. Теперь узнАем,

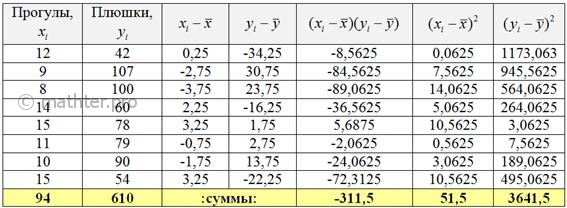
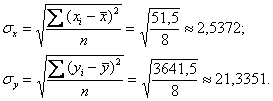
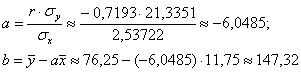
7.3.5. Как решить задачу в случае комбинационной группировки

7.3.3. Коэффициент детерминации

| Оглавление |