Ваш репетитор, справочник и друг!

Кратчайший курс школьной математики

1.1. Числа. Кратко о главном

Во-первых, не следует путать числа с цифрами.

Цифры – это числовые символы, с помощью которых записывают числа. Наиболее известны арабские цифры: и римские цифры: .

Ну а числа – это числа :)

Исторически первыми появились натуральные числа, предназначенные для подсчёта материальных объектов (людей, кур, овец, монет и т.д.):

, для краткости множество натуральных чисел обозначают утолщённой, стилизованной или жирной буквой .

И полезно будет вспомнить римский вариант:

Иногда к множеству натуральных чисел относят ноль: .

Справка: элементы произвольного множества принято записывать в фигурных скобках . Если множество не содержит элементов, то его называют пустым и обозначают символом . Значок символизирует принадлежность множеству.

Если к множеству присоединить те же числа с противоположным знаком и ноль, то получится множество целых чисел:

, оптимизаторы и лентяи записывают его элементы со значками «плюс минус»:

Совершенно понятно, что натуральные числа являются подмножеством множества целых чисел: (значок называют значком включения). Название множества тоже «говорящее»: целые числа – это значит, никаких дробей.

И, коль скоро, целые, то сразу же вспомним важные признаки их делимости на 2, 3, 5 и 10, которые будут требоваться в практических вычислениях чуть ли не каждый день:

1) Целое число делится на 2 без остатка, если оно заканчивается на 0, 2, 4, 6 или 8. Например, числа 400, -1502, -24, 66996, 818 – делятся на 2 без остатка.

Если целое число делится на 2 без остатка, то его называют чётным, в противном случае оно нечётное. Ноль – это чётное число (т.к. делится на два без остатка).

2) С делимость на 3 чуть сложнее: целое число делится на 3 без остатка, если сумма входящих в него цифр делится на 3. Примеры:

Проверим, делится ли на 3 число 27901. Для этого просуммируем его цифры:
2 + 7 + 9 + 0 + 1 = 19 – не делится на 3
Вывод: 27901 не делится на 3.

Просуммируем цифры числа -825432:
8 + 2 + 5 + 4 + 3 + 2 = 24 – делится на 3
Вывод: число -825432 делится на 3

3) Целое число делится на 5, если оно заканчивается пятёркой либо нулём:

775, -2390 – делятся на 5

4) Целое число делится на 10, если оно заканчивается на ноль:

798400 – делится на 10 (и, очевидно, на 100). Ну и, наверное, все помнят – для того, чтобы разделить на 10, нужно просто убрать один ноль: 79840

Также существуют признаки делимости на 4, 6, 8, 9, 11 и т.д., но практического толка от них практически нет =)

Следующим числовым множеством идёт множество рациональных чисел:
– то есть, любое рациональное число представимо в виде обыкновенной дроби с целым числителем (верх) и натуральным знаменателем (низ).

Немедленно повторим понятие положительной обыкновенной дроби. Представьте торт, который можно разрезать на любое количество равных кусков. …Почему торт? Потому что в нём мало букв :). Итак, торт – это единица. Интерпретируем дроби:
– торт разрезали на 3 равных куска, взяли 2 куска (две третьих);
– торт разрезали на 5 равных кусков, взяли 1 кусок (одну пятую);
– торт разрезали на 7 равных кусков, взяли 6 кусков (шесть седьмых).

Обратите внимание, что числитель любой из этих дробей меньше знаменателя. Такие дроби называют правильными. Правильная дробь обязательно меньше единицы. Если же мы берём все куски торта или больше, то дробь будет неправильной:
– торт разрезали на 10 равных куска, взяли 10 кусков (один торт);
– торт разрезали на 4 равных куска, взяли 4 куска и от второго торта взяли ещё 3 таких же куска. Итого, семь четвёртыхили: – одна целая три четверти. Дроби с целой и дробной частью (например, ) называют смешанными.
Характерным «опознавательным» признаком рационального числа является то обстоятельство, что при делении числителя на знаменатель получается:
либо – целое число, либо – конечная десятичная дробь, либо
– бесконечная периодическая десятичная дробь (повтор может начаться не сразу).

Полюбуйтесь этим делением и постарайтесь так делать как можно реже! Это не мантра, и даже не золотое правило – это самая настоящая практическая аксиома, которую я не устану повторять в будущем:

В высшей математике все действия стремимся выполнять
в обыкновенных (правильных и неправильных) дробях

Согласитесь, что иметь дело с дробью значительно удобнее, чем с десятичным вариантом 0,375 (не говоря уже о бесконечных дробях). О том, как перевести десятичную дробь в обыкновенную, поговорим чуть позже.

Помимо рациональных существует множество иррациональных чисел, каждое из которых представИмо в виде бесконечной НЕпериодической десятичной дроби. Иными словами, в бесконечных «хвостах» иррациональных чисел нет никакой закономерности:

(«год рождения Льва Толстого» дважды)
и так далее.

О знаменитых константах «пи» и «е» информации предостаточно, поэтому на них я не останавливаюсь. Из всей этой информации желательно помнить хотя бы 2-3 знака после запятой: (значок означает «приблизительно равно»).

Повторим заодно правило округления десятичных дробей: при округлении дроби до некоторого знака после запятой, нужно посмотреть на следующий разряд: если там 0, 1, 2 или 4, то число округляется в меньшую сторону, если же там 5, 6, 7, 8 или 9, то число округляется в бОльшую сторону. Так, при округлении числа до двух знаков после запятой смотрим на разряд тысячных: там 1, поэтому округляем в меньшую сторону: . Теперь округлим «пи» до трёх знаков после запятой – смотрим на следующий разряд: 5, поэтому округляем в бОльшую сторону: . При округлении до четырёх знаков после запятой опять округляем в бОльшую сторону: (поскольку в следящем разряде 9). Едем дальше:

Объединение рациональных и иррациональных чисел образует множество действительных (вещественных) чисел:

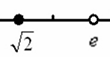
Справка: – значок объединения множеств.
Геометрическая интерпретация множества вам хорошо знакома – это числовая прямая или числовая ось:

Каждому действительному числу соответствует определённая точка числовой прямой, и наоборот – каждой точке числовой прямой обязательно соответствует некоторое действительное число.

Числовую ось обозначают буквами , где буква символически совмещается с нулём. Точка называется началом координат. Числовую прямую также обозначают бесконечным интервалом ( – значок бесконечности).

Запись или эквивалентная ей запись символизирует тот факт, что принадлежит множеству действительных чисел (или попросту, «икс» – действительное число). …Ну вот мы и добрались до «иксов» J

В различных задачах часто рассматривают следующие числовые промежутки:

конечные интервалы, например, , полуинтервалы, а-ка и ,
и отрезки, .

Справка: круглая скобка означает то, что крайнее значение не входит в промежуток, а квадратная то – что входит.

Значения, которые не входят в промежуток обозначают выколотыми точками:

интервал ,

полуинтервал ,

полуинтервал ,

отрезок .

И в заключение параграфа ещё одно важное понятие. Его недопонимают, его недолюбливают, но мы преодолеем эти комплексы!

Модуль или абсолютное значение числа – это его расстояние от начала координат. Так как расстояние не может быть отрицательным, то модуль любого числа больше либо равен нулю. Грубо говоря, модуль «уничтожает» возможный знак «минус»:
и т.д.

Числа, равные по модулю (например, 4 и –4), называют противоположными. Такие числа равноудалены от начала координат (от нуля).

Расстояние между двумя числами равно модулю их разности, например: , причём, вычитать можно в любом порядке: .

Пожалуй, пока достаточно…, и к модулю мы ещё обязательно вернёмся!

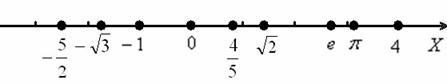
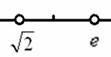
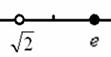
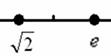
1.2. Буквы в математике

| Оглавление |