1.2.2. Совместные и несовместные события.
Противоположные события. Полная группа событий
События называют несовместными, если в одном и том же испытании появление одного из событий исключает появление других событий. Простейшим примером несовместных событий является пара противоположных событий. Событие, противоположное данному, обычно обозначается той же латинской буквой с чёрточкой наверху:
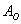 – в результате броска монеты выпадет орёл; – в результате броска монеты выпадет орёл;
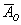 – в результате этого же броска выпадет решка. – в результате этого же броска выпадет решка.
Совершено ясно, что в отдельно взятом испытании появление орла исключает появление решки (и наоборот), поэтому данные события и называются несовместными.
Противоположные события легко формулируются из соображений элементарной логики:
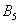 – в результате броска игрального кубика выпадет 5 очков; – в результате броска игрального кубика выпадет 5 очков;
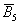 – в результате этого же броска выпадет число очков, отличное от пяти. – в результате этого же броска выпадет число очков, отличное от пяти.
Либо 5, либо не 5, т.е. данные события несовместны и противоположны.
Аналогично:
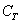 – из колоды будет извлечена карта трефовой масти, либо: – из колоды будет извлечена карта трефовой масти, либо:
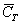 – извлечена пика, черва или бубна. – извлечена пика, черва или бубна.
Множество несовместных событий образуют полную группу, если в результате отдельно взятого испытания обязательно появится одно и только одно из этих событий. Очевидно, что любая пара противоположных событий, например, 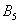 и и 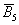 (выпадение / невыпадение «пятёрки») образует полную группу. Но, разумеется, полную группу могут образовывать не только противоположные события: (выпадение / невыпадение «пятёрки») образует полную группу. Но, разумеется, полную группу могут образовывать не только противоположные события:
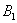 – в результате броска игрального кубика выпадет 1 очко; – в результате броска игрального кубика выпадет 1 очко;
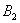 – … 2 очка; – … 2 очка;
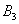 – … 3 очка; – … 3 очка;
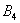 – … 4 очка; – … 4 очка;
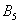 – … 5 очков; – … 5 очков;
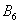 – … 6 очков. – … 6 очков.
События 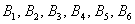 несовместны (поскольку появление какой-либо грани исключает одновременное появление других) и образуют полную группу (так как в результате испытания обязательно появится одно из этих шести событий). несовместны (поскольку появление какой-либо грани исключает одновременное появление других) и образуют полную группу (так как в результате испытания обязательно появится одно из этих шести событий).
И из этих двух примеров вытекает ещё одно важное понятие, которое нам потребуется в дальнейшем – это элементарность исхода (события). Если совсем просто, то элементарное событие нельзя «разложить на другие события». Например, события 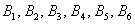 элементарны, но событие элементарны, но событие 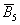 не является таковым, так как подразумевает выпадение 1, 2, 3, 4 или 6 очков (включает в себя 5 элементарных исходов). не является таковым, так как подразумевает выпадение 1, 2, 3, 4 или 6 очков (включает в себя 5 элементарных исходов).
В примере с картами события 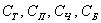 (извлечение трефы, пики, червы или бубны соответственно) несовместны и образуют полную группу, но они неэлементарны. Если считать, что в колоде 36 карт, то каждое из перечисленных выше событий включает в себя 9 элементарных исходов. Аналогично – события (извлечение трефы, пики, червы или бубны соответственно) несовместны и образуют полную группу, но они неэлементарны. Если считать, что в колоде 36 карт, то каждое из перечисленных выше событий включает в себя 9 элементарных исходов. Аналогично – события 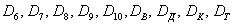 (извлечение шестёрки, семёрки, …, короля, туза) несовместны, образуют полную группу и неэлементарны (каждое включает в себя 4 исхода). (извлечение шестёрки, семёрки, …, короля, туза) несовместны, образуют полную группу и неэлементарны (каждое включает в себя 4 исхода).
Таким образом, элементарным исходом здесь считается лишь извлечение какой-то конкретной карты, и 36 несовместных элементарных исходов тоже образуют полную группу событий.
И коротко о событиях совместных. События называются совместными, если в отдельно взятом испытании появление одного из них не исключает появление другого. Например:
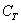 – из колоды карт будет извлечена трефа; – из колоды карт будет извлечена трефа;
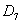 – из колоды карт будет извлечена семёрка. – из колоды карт будет извлечена семёрка.
– данные события совместны, т.к. при излечении семёрки треф одновременно имеют место оба события.
Понятие совместности охватывает и бОльшее количество событий:
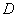 – завтра в 12.00 будет дождь; – завтра в 12.00 будет дождь;
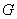 – завтра в 12.00 будет гроза; – завтра в 12.00 будет гроза;
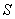 – завтра в 12.00 будет солнце. – завтра в 12.00 будет солнце.
Ситуация, конечно, редкая, но совместное появление всех трёх событий, не исключено. Следует отметить, что перечисленные события совместны и попарно.
 1.2.3. Сложение и умножение событий 1.2.3. Сложение и умножение событий
 1.2.1. Виды событий 1.2.1. Виды событий
| Оглавление |
|