1.5. Геометрическое определение вероятности
Классическое определение вероятности оказывается эффективным для решения целого спектра задач, но с другой стороны, обладает и рядом ограничений. Одним из таких ограничений является тот факт, что оно неприменимо к испытаниям с бесконечным количеством исходов. Простейший пример:
На отрезок 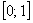 наудачу бросается точка. Какова вероятность того, что она попадёт в промежуток наудачу бросается точка. Какова вероятность того, что она попадёт в промежуток 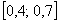 ? ?

Поскольку на отрезке бесконечно много точек, то здесь нельзя применить формулу 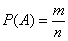 (ввиду бесконечно большого значения «эн») и поэтому на помощь приходит другой подход, называемый геометрическим определением вероятности: (ввиду бесконечно большого значения «эн») и поэтому на помощь приходит другой подход, называемый геометрическим определением вероятности:
На практике в качестве такой геометрической меры чаще всего выступает длина или площадь, реже – объём.
Рассмотрим событие: 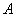 – брошенная на отрезок – брошенная на отрезок 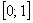 точка, попала в промежуток точка, попала в промежуток 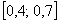 . Очевидно, что общее число исходов выражается длиной бОльшего отрезка: . Очевидно, что общее число исходов выражается длиной бОльшего отрезка: 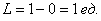 , а благоприятствующие событию , а благоприятствующие событию 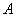 исходы – длиной вложенного отрезка: исходы – длиной вложенного отрезка: 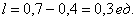 По геометрическому определению вероятности: По геометрическому определению вероятности:
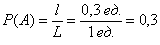
Примечание: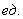 – метрические единицы: метры, сантиметры или какие-то др. – метрические единицы: метры, сантиметры или какие-то др.
Слишком просто? Как и в случае с классическим определением, это обманчивое впечатление. Обстоятельно и добросовестно разбираемся в практических примерах:
Задача 28
Метровую ленту случайным образом разрезают ножницами. Найти вероятность того, что длина обрезка составит не менее 80 см.
Решение: «чего тут сложного? Вероятность равна 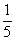 ». Это автоматическая ошибка, которую допускают по небрежности. Да, совершенно верно – длина обрезка составит не менее 80 см, если от ленты отрезать меньше 20 сантиметров. Но здесь часто забывают, что искомый разрез можно сделать как с одного конца ленты, так и с другого: ». Это автоматическая ошибка, которую допускают по небрежности. Да, совершенно верно – длина обрезка составит не менее 80 см, если от ленты отрезать меньше 20 сантиметров. Но здесь часто забывают, что искомый разрез можно сделать как с одного конца ленты, так и с другого:
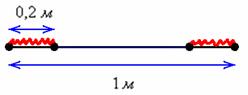
Рассмотрим событие: 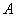 – длина обрезка составит не менее 0,8 м. – длина обрезка составит не менее 0,8 м.
Поскольку ленту можно разрезать где угодно, то общему числу исходов соответствует её длина: 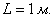 Благоприятствующим исходам соответствуют участки, отмеченные красным цветом, и их суммарная длина равна: Благоприятствующим исходам соответствуют участки, отмеченные красным цветом, и их суммарная длина равна: 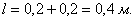
По геометрическому определению:
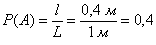
Ответ: 0,4
Какой можно сделать вывод?
Даже если задача кажется вам очень простой, НЕ СПЕШИТЕ
При оформлении задач следует обязательно указывать размерность (единицы, метры, квадратные единицы, квадратные метры и т.д.). Кстати, обратите внимание, что на финальном этапе вычислений геометрическая мера сокращается. Так в рассмотренном примере, сократились метры:
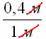 , в результате чего получилась привычная безразмерная вероятность. , в результате чего получилась привычная безразмерная вероятность.
Следующая задача для самостоятельного решения:
Задача 29
После бури на участке между 40-м и 70-м километрами телефонной линии произошёл обрыв провода. Какова вероятность того, что он произошёл между 50-м и 55-м километрами линии?
Значительно чаще встречаются примеры, в которых фигурируют площади:
Задача 30
В треугольник со сторонами 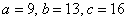 вписан круг. Точка вписан круг. Точка 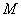 произвольно ставится в треугольник. Найти вероятность того, что точка попадёт в круг. произвольно ставится в треугольник. Найти вероятность того, что точка попадёт в круг.
Вспоминаем геометрию: вписанный круг лежит внутри треугольника и касается его сторон в трёх точках. …Представили? Отлично!
Решение: поскольку точка ставится в треугольник, а круг лежит внутри, то общему числу исходов соответствует площадь треугольника, а множеству благоприятствующих исходов – площадь вписанного круга.
Осталось вспомнить или отыскать (проще всего в Сети) школьные геометрические формулы. Если даны длины сторон треугольника, то его площадь удобно найти по формуле Герона:
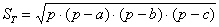 , где , где 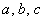 – длины сторон треугольника, а – длины сторон треугольника, а 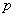 – полупериметр. – полупериметр.
Сначала вычислим полупериметр треугольника: 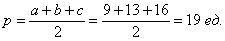 , а затем его площадь: , а затем его площадь:
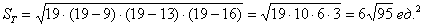
Площадь круга найдём по известной формуле 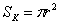 . Если круг вписан в треугольник, то его радиус можно рассчитать по формуле . Если круг вписан в треугольник, то его радиус можно рассчитать по формуле 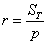 , этого я не вообще не знал – только что нашёл в Интернете. , этого я не вообще не знал – только что нашёл в Интернете.
Итак, площадь вписанного круга:
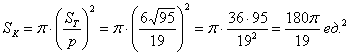
По геометрическому определению:
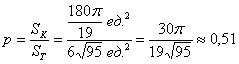 – вероятность того, что точка – вероятность того, что точка 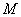 попадёт во вписанный круг. попадёт во вписанный круг.
Ответ: 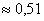
Более простой пример для самостоятельного решения:
Задача 31
В круге радиуса 10 см находится прямоугольный треугольник с катетами 12 и 7 см. В круг наудачу ставится точка. Найти вероятность того, что она не попадёт в данный треугольник.
Следует отметить, что в этой задаче треугольник вовсе не обязан как-то касаться окружности, он просто расположен внутри круга и всё. Будьте внимательны!
А теперь рассмотрим широко известную задачу о встрече:
Задача 32
Две грузовые машины могут подойти на погрузку в промежуток времени от 19.00 до 20.30. Погрузка первой машины длится 10 минут, второй – 15 минут. Какова вероятность того, что одной машине придется ждать окончания погрузки другой?
Решение: сначала выясним длительность временнОго промежутка, на котором могут пересечься автомобили: это 90 минут (коль скоро, от 19.00 до 20.30). Изобразим прямоугольную систему координат, где в подходящем масштабе построим квадрат размером 90 на 90 единиц:
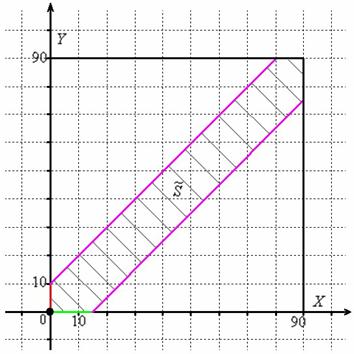
Общему множеству исходов соответствует площадь данного квадрата:
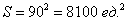
Далее по оси 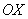 от начала координат откладываем время погрузки одного автомобиля (зелёная линия), а по оси от начала координат откладываем время погрузки одного автомобиля (зелёная линия), а по оси 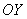 – время погрузки другого автомобиля (красная линия) (можно наоборот, это не повлияет на решение). – время погрузки другого автомобиля (красная линия) (можно наоборот, это не повлияет на решение).
Теперь из правого конца зелёного отрезка и из верхнего конца красного отрезка под углом 45 градусов проводим две линии внутри квадрата (малиновые отрезки).
Множеству благоприятствующих исходов (когда автомобили «пересекутся» во времени) соответствует площадь 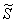 заштрихованной фигуры. В принципе, её можно вычислить «на пальцах», но технически проще использовать окольный путь, а именно, вычислить площади двух прямоугольных треугольников. Используем формулу: заштрихованной фигуры. В принципе, её можно вычислить «на пальцах», но технически проще использовать окольный путь, а именно, вычислить площади двух прямоугольных треугольников. Используем формулу:
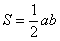 , где , где 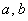 – длины катетов. – длины катетов.
В нашей задаче: верхний треугольник имеет катеты длиной по 80 единиц, нижний треугольник – по 75 единиц. Обратите внимание, что в общем случае эти треугольники не равны.
Таким образом, суммарная площадь треугольников составляет:
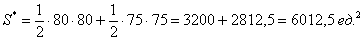
И бесхитростный заключительный манёвр: из площади квадрата вычитаем площади треугольников, получая тем самым благоприятствующую площадь:
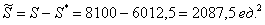
По геометрическому определению:
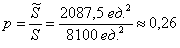 – вероятность того, что одной машине придется ждать окончания погрузки другой. – вероятность того, что одной машине придется ждать окончания погрузки другой.
Ответ: 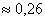
Подробное объяснение этого способа решения можно найти, например, в учебном пособии В.Е. Гмурмана, я же остановился лишь на техническом алгоритме, дабы не тратить ваше драгоценное время.
И если в разобранной задаче встреча явно нежелательна, то в следующей, скорее, наоборот. Романтичный эпизод для самостоятельного изучения:
Задача 33
Студенты случайным образом приходят в столовую с 14.00 до 15.00, при этом обед каждого из них занимает примерно 20 минут. Найти вероятность того, что: а) Коля встретится с Олей во время обеда, б) данная встреча не состоится.
Не нужно печалиться по поводу пункта «бэ» – любовь приходит и уходит, а кушать хочется всегда! =)
Решение, чертёж и ответ в конце книги.
Оставшиеся примеры параграфа посвящены не менее распространённому типу задач, где фигурируют неравенства.
Для начала разогревающий пример:
Задача 34
В квадрат с вершинами 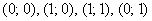 наудачу брошена точка наудачу брошена точка 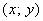 . Найдите вероятность того, что координаты этой точки удовлетворяют неравенству . Найдите вероятность того, что координаты этой точки удовлетворяют неравенству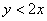 . .
Решение: изобразим на чертеже искомый квадрат и прямую 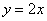 : :
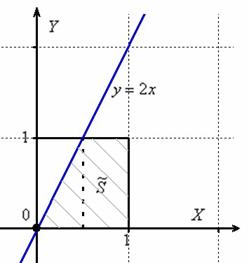
Общему множеству исходов соответствует площадь квадрата 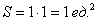
Прямая 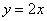 делит квадрат на треугольник и трапецию. Как определить фигуру, которая удовлетворяет условию делит квадрат на треугольник и трапецию. Как определить фигуру, которая удовлетворяет условию 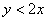 ? Вспоминаем линейные неравенства: нужно взять любую точку, не принадлежащую прямой ? Вспоминаем линейные неравенства: нужно взять любую точку, не принадлежащую прямой 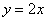 , например, точку , например, точку 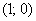 и подставить её координаты в неравенство: и подставить её координаты в неравенство:
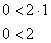
Получено верное неравенство, значит, множеству благоприятствующих исходов соответствует площадь 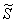 трапеции. Рассчитаем данную площадь как сумму площадей прямоугольного треугольника и прямоугольника (разделены на чертеже пунктиром): трапеции. Рассчитаем данную площадь как сумму площадей прямоугольного треугольника и прямоугольника (разделены на чертеже пунктиром):
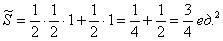
По геометрическому определению:
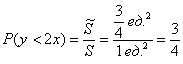 – вероятность того, что координаты брошенной в данный квадрат точки удовлетворяют неравенству – вероятность того, что координаты брошенной в данный квадрат точки удовлетворяют неравенству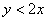 . .
Ответ: 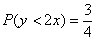
…аналитическую геометрию немного вспомнили, теперь на очереди математический анализ, ибо неравенства бывают не только линейными:
Задача 35
Загадываются два числа 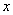 и и 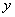 в промежутке от 0 до 5. Какова вероятность, что в промежутке от 0 до 5. Какова вероятность, что 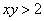 ? ?
Схема решения уже знакома: коль скоро загадываются 2 произвольных числа от нуля до пяти (они могут быть и иррациональными), то общему количеству исходов соответствует площадь квадрата 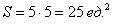
Изобразим ветвь гиперболы 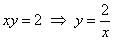 , которая делит квадрат на две части: , которая делит квадрат на две части:
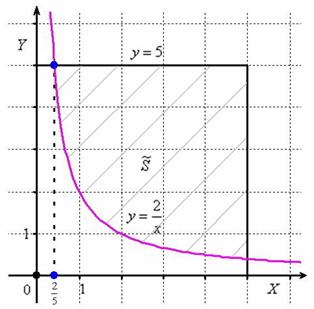
Теперь выясним, какой из этих двух «кусков» удовлетворяет неравенству 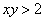 . Для этого выберем любую точку, не принадлежащую гиперболе, проще всего взять . Для этого выберем любую точку, не принадлежащую гиперболе, проще всего взять 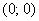 , и подставим её координаты в наше неравенство: , и подставим её координаты в наше неравенство:
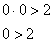
Получено неверное неравенство, а значит, условию 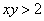 соответствует «верхний кусок», площадь соответствует «верхний кусок», площадь 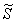 которого, деваться тут некуда, придётся вычислить с помощью определённого интеграла. Уточним нижний предел интегрирования аналитически (найдём точку пересечения гиперболы которого, деваться тут некуда, придётся вычислить с помощью определённого интеграла. Уточним нижний предел интегрирования аналитически (найдём точку пересечения гиперболы 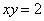 и прямой и прямой 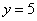 ): ):
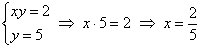
На отрезке 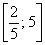 прямая прямая 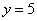 расположена не ниже гиперболы расположена не ниже гиперболы 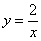 , по соответствующей формуле: , по соответствующей формуле:
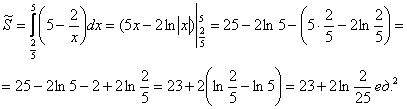
По геометрическому определению:
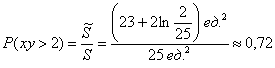 – вероятность того, что произведение двух загаданных в промежутке от 0 до 5 чисел окажется больше двух. – вероятность того, что произведение двух загаданных в промежутке от 0 до 5 чисел окажется больше двух.
Ответ: 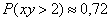
Аналогичный пример для самостоятельного решения:
Задача 36
Загадываются два числа 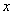 и и 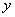 в промежутке от 0 до 10. Какова вероятность, что в промежутке от 0 до 10. Какова вероятность, что 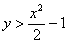 ? ?
Данная задача (как, собственно, и предыдущая) допускает несколько способов расчёта площади, подумайте, какой путь более рационален.
В заключение следует отметить, что геометрическое определение вероятности тоже обладает своими недостатками. Один из них заключается в своеобразном парадоксе, давайте вспомним самый первый пример с отрезком 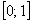 , на который случайным образом падает точка. Возможно ли, что точка попадёт, например, на самый край отрезка? Да, такое событие возможно, но по геометрическому определению, его вероятность равна нулю! И то же самое можно сказать о любой точке отрезка! Дело в том, что с позиций геометрии размеры отдельно взятой точки равны нулю, и поэтому геометрическое определение вероятности здесь не срабатывает. , на который случайным образом падает точка. Возможно ли, что точка попадёт, например, на самый край отрезка? Да, такое событие возможно, но по геометрическому определению, его вероятность равна нулю! И то же самое можно сказать о любой точке отрезка! Дело в том, что с позиций геометрии размеры отдельно взятой точки равны нулю, и поэтому геометрическое определение вероятности здесь не срабатывает.
 1.6.1. Теорема сложения вероятностей несовместных событий 1.6.1. Теорема сложения вероятностей несовместных событий
 1.4. Классическое определение вероятности 1.4. Классическое определение вероятности
| Оглавление |
|

 Практикум по теории вероятностей
Практикум по теории вероятностей Научись решать в считанные дни!
Научись решать в считанные дни!

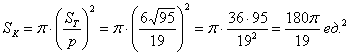
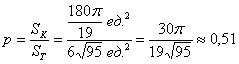 – вероятность того, что точка
– вероятность того, что точка 

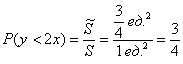 – вероятность того, что координаты брошенной в данный квадрат точки удовлетворяют неравенству
– вероятность того, что координаты брошенной в данный квадрат точки удовлетворяют неравенству
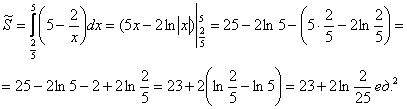
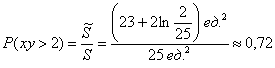 – вероятность того, что произведение двух загаданных в промежутке от 0 до 5 чисел окажется больше двух.
– вероятность того, что произведение двух загаданных в промежутке от 0 до 5 чисел окажется больше двух. 1.6.1. Теорема сложения вероятностей несовместных событий
1.6.1. Теорема сложения вероятностей несовместных событий 1.4. Классическое определение вероятности
1.4. Классическое определение вероятности