1.4. Классическое определение вероятности
Вероятностью наступления события 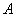 в некотором испытании называют отношение в некотором испытании называют отношение 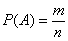 , где: , где:
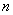 – общее число всех равновозможных, элементарных исходов этого испытания, которые образуют полную группу событий; – общее число всех равновозможных, элементарных исходов этого испытания, которые образуют полную группу событий;
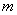 – количество элементарных исходов, благоприятствующих событию – количество элементарных исходов, благоприятствующих событию 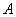 . .
При броске монеты может выпасть либо орёл, либо решка – данные события образуют полную группу, таким образом, общее число исходов 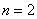 ; при этом, каждый из них элементарен и равновозможен. Событию ; при этом, каждый из них элементарен и равновозможен. Событию 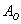 благоприятствует благоприятствует 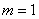 исход (выпадение орла). По классическому определению вероятностей: исход (выпадение орла). По классическому определению вероятностей: 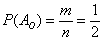 . .
Аналогично, в результате броска кубика может появиться 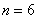 элементарных равновозможных исходов, образующих полную группу, а событию элементарных равновозможных исходов, образующих полную группу, а событию 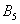 благоприятствует единственный благоприятствует единственный 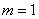 исход (выпадение пятёрки). Поэтому исход (выпадение пятёрки). Поэтому 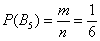 . .
Особое внимание обращаю на третий пример. Здесь будет некорректным сказать «раз в колоде 4 масти, то вероятность извлечения трефы 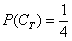 ». В определении речь идёт об элементарных исходах, поэтому правильный порядок рассуждений таков: всего в колоде 36 карт (несовместные элементарные исходы, образующие полную группу), из них 9 карт трефовой масти (количество благоприятствующих событию ». В определении речь идёт об элементарных исходах, поэтому правильный порядок рассуждений таков: всего в колоде 36 карт (несовместные элементарные исходы, образующие полную группу), из них 9 карт трефовой масти (количество благоприятствующих событию 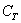 исходов); по классическому определению вероятности: исходов); по классическому определению вероятности: 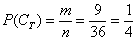 . Именно так! . Именно так!
«Крайние» значения вероятности (ноль и единица) получаются посредством точно таких же рассуждений. Пусть из некой урны, в которой находятся 10 красных шаров, наугад извлекается 1 шар. Рассмотрим следующие события:
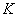 – из урны будет извлечён красный шар; – из урны будет извлечён красный шар;
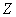 – из урны будет извлечён зелёный шар. – из урны будет извлечён зелёный шар.
Общее количество исходов: 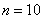 . .
Событию 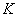 благоприятствуют все возможные исходы благоприятствуют все возможные исходы 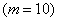 , следовательно, , следовательно, 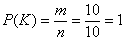 , то есть данное событие достоверно. Для 2-го же события благоприятствующие исходы отсутствуют , то есть данное событие достоверно. Для 2-го же события благоприятствующие исходы отсутствуют 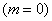 , поэтому , поэтому 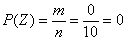 , то есть событие , то есть событие 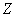 невозможно. невозможно.
НЕ ПРОПУСКАЕМ задачи! Особенно, если они кажутся элементарными.
Задача 16
В урне находится 15 белых, 5 красных и 10 чёрных шаров. Наугад извлекается 1 шар, найти вероятность того, что он будет: а) белым, б) красным, в) чёрным.
Важнейшей предпосылкой для использования классического определения вероятности является возможность подсчёта общего количества исходов.
И решение как раз с этого и начинается, всего в урне:
15 + 5 + 10 = 30 шаров, при этом справедливы следующие факты:
– извлечение любого шара одинаково возможно (равновозможность исходов), при этом исходы элементарны и образуют полную группу событий (т.е. в результате испытания обязательно будет извлечён какой-то один из 30 шаров).
Таким образом, общее число исходов: 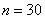 . .
Рассмотрим событие: 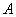 – из урны будет извлечён белый шар. Данному событию благоприятствуют – из урны будет извлечён белый шар. Данному событию благоприятствуют 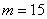 элементарных исходов, поэтому по классическому определению: элементарных исходов, поэтому по классическому определению:
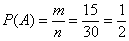 – вероятность того, что из урны будет извлечён белый шар. – вероятность того, что из урны будет извлечён белый шар.
Как ни странно, даже в такой простой задаче можно допустить серьёзную неточность, на которой я уже заострял внимание. В чём здесь подводный камень? Здесь некорректно рассуждать, что «раз половина шаров белые, то вероятность извлечения белого шара 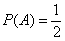 ». ».
В классическом определении вероятности речь идёт об ЭЛЕМЕНТАРНЫХ исходах, и дробь 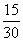 следует обязательно прописать! следует обязательно прописать!
С другими пунктами аналогично, рассмотрим следующие события:
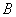 – из урны будет извлечён красный шар; – из урны будет извлечён красный шар;
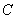 – из урны будет извлечён чёрный шар. – из урны будет извлечён чёрный шар.
Событию 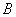 благоприятствует 5 элементарных исходов, а событию благоприятствует 5 элементарных исходов, а событию 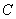 – 10 элементарных исходов. Таким образом, соответствующие вероятности: – 10 элементарных исходов. Таким образом, соответствующие вероятности:
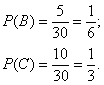
Типичная проверка многих задач по терверу осуществляется с помощью теоремы о сумме вероятностей событий, образующих полную группу. В нашем случае события 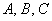 образуют полную группу, а значит, сумма соответствующих вероятностей должна обязательно равняться единице: образуют полную группу, а значит, сумма соответствующих вероятностей должна обязательно равняться единице: 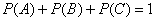 . .
Проверим, так ли это: 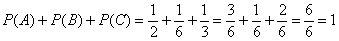 , в чём и хотелось убедиться. , в чём и хотелось убедиться.
Ответ: 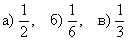 – в ответе достаточно записать лишь числа. – в ответе достаточно записать лишь числа.
На практике распространён «скоростной» вариант оформления решения:
Всего: 15 + 5 + 10 = 30 шаров в урне. По классическому определению:
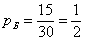 – вероятность того, то из урны будет извлечён белый шар; – вероятность того, то из урны будет извлечён белый шар;
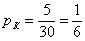 – вероятность того, то из урны будет извлечён красный шар; – вероятность того, то из урны будет извлечён красный шар;
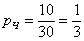 – вероятность того, то из урны будет извлечён чёрный шар. – вероятность того, то из урны будет извлечён чёрный шар.
Ответ: 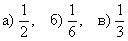
Однако, если в условии несколько пунктов, то решение зачастую удобнее оформить первым способом, который отнимает чуть больше времени, но зато всё «раскладывает по полочкам» и позволяет легче сориентироваться в задаче.
Задача 17
В магазин поступило 30 холодильников, пять из которых имеют заводской дефект. Случайным образом выбирают один холодильник. Какова вероятность того, что он будет без дефекта?
Это пример для самостоятельного решения. Выберите целесообразный вариант оформления и сверьтесь с образцом в конце книги.
В простейших случаях количество общих и количество благоприятствующих исходов «лежат на поверхности», но чаще их приходится добывать самостоятельно. Каноничная серия задач о забывчивом абоненте:
Задача 18
Набирая номер телефона, абонент забыл две последние цифры, но помнит, что одна из них ноль, а другая нечётная. Найти вероятность того, что он наберёт правильный номер
Примечание: ноль – это чётное число (делится на 2 без остатка)
Решение: сначала найдём общее количество исходов. Привлекаем на помощь комбинаторику:
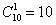 способами можно набрать предпоследнюю цифру; способами можно набрать предпоследнюю цифру;
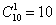 способами можно набрать последнюю цифру. способами можно набрать последнюю цифру.
По правилу умножения комбинаций: 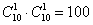 способами можно набрать предпоследнюю цифру и последнюю цифру. способами можно набрать предпоследнюю цифру и последнюю цифру.
В целях повторения расшифруем эту запись другим способом: «каждая цифра на предпоследнем месте комбинируется с каждой цифрой на последнем месте, и таких комбинаций сто»
Как вариант, можно использовать формулу количества размещений с повторениями: 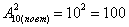 способами можно составить упорядоченный набор из двух цифр, причём цифры могут оказаться и одинаковыми. способами можно составить упорядоченный набор из двух цифр, причём цифры могут оказаться и одинаковыми.
По возможности всегда старайтесь анализировать найденное множество исходов. ЧТО это за комбинации и действительно ли их ТАКОЕ количество? В данной задаче ответ на эти вопросы элементарен:
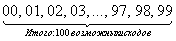
С общим количеством исходов разобрались, теперь благоприятствующие исходы. По условию, абонент помнит, что одна из цифр – ноль, а другая цифра – нечётная. Здесь рациональнее не мудрить с комбинаторикой и воспользоваться методом прямого перечисления исходов. То есть, при оформлении решения просто записываем все благоприятствующие комбинации:
01, 03, 05, 07, 09
10, 30, 50, 70, 90
и подсчитываем их – всего: 10 благоприятствующих исходов.
По классическому определению:
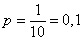 – вероятность того, что абонент наберёт правильный номер – вероятность того, что абонент наберёт правильный номер
Ответ: 0,1
Десятичные дроби в тервере смотрятся вполне уместно, но можно придерживаться и традиционного вышматовского стиля, оперируя только обыкновенными дробями.
Продвинутая задача для самостоятельного решения:
Задача 19
Абонент забыл пин-код к своей сим-карте, однако помнит, что он содержит три «пятёрки», а одна из цифр – то ли «семёрка», то ли «восьмёрка». Какова вероятность включить телефон с первой попытки?
Иногда в задаче не просматривается явное комбинаторное решение, и перечисление всех комбинаций (фактически вынужденное) оказывается весьма кропотливым занятием. В частности, так обстоят дела в следующей, не менее популярной группе задач, где подкидываются 2 игральных кубика (реже – бОльшее количество):
Задача 20
Найти вероятность того, что при бросании двух игральных костей в сумме выпадет:
а) пять очков;
б) не более четырёх очков;
в) от 3 до 9 очков включительно.
Решение: найдём общее количество исходов:
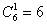 способами может выпасть грань 1-го кубика и способами может выпасть грань 1-го кубика и 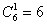 способами может выпасть грань 2-го кубика; по правилу умножения комбинаций, всего: способами может выпасть грань 2-го кубика; по правилу умножения комбинаций, всего: 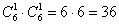 возможных комбинаций. Иными словами, каждая грань 1-го кубика может составить упорядоченную пару с каждой гранью 2-го кубика. Условимся записывать такую пару в виде возможных комбинаций. Иными словами, каждая грань 1-го кубика может составить упорядоченную пару с каждой гранью 2-го кубика. Условимся записывать такую пару в виде 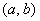 , где , где 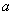 – цифра, выпавшая на 1-м кубике, – цифра, выпавшая на 1-м кубике, 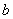 – цифра, выпавшая на 2-м кубике. Например: – цифра, выпавшая на 2-м кубике. Например:
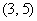 – на первом кубике выпало 3 очка, на втором – 5 очков, их сумма: 3 + 5 = 8; – на первом кубике выпало 3 очка, на втором – 5 очков, их сумма: 3 + 5 = 8;
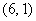 – на первом кубике выпало 6 очков, на втором – 1 очко, их сумма: 6 + 1 = 7; – на первом кубике выпало 6 очков, на втором – 1 очко, их сумма: 6 + 1 = 7;
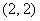 – на обеих костях выпало 2 очка, сумма: 2 + 2 = 4. – на обеих костях выпало 2 очка, сумма: 2 + 2 = 4.
Очевидно, что наименьшую сумму даёт пара 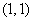 , а наибольшую – пара , а наибольшую – пара 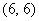 . .
а) Рассмотрим событие: 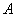 – в результате броска двух игральных костей выпадет 5 очков. Запишем и подсчитаем количество исходов, которые благоприятствуют данному событию: – в результате броска двух игральных костей выпадет 5 очков. Запишем и подсчитаем количество исходов, которые благоприятствуют данному событию:
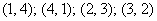
Итого: 4 благоприятствующих исхода.
По классическому определению:
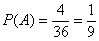 – искомая вероятность. – искомая вероятность.
б) Рассмотрим событие: 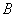 – выпадет не более 4 очков. То есть, либо 2, либо 3, либо 4 очка. Снова перечисляем и подсчитываем благоприятствующие комбинации, слева я буду записывать суммарное количество очков, а после двоеточия – подходящие пары: – выпадет не более 4 очков. То есть, либо 2, либо 3, либо 4 очка. Снова перечисляем и подсчитываем благоприятствующие комбинации, слева я буду записывать суммарное количество очков, а после двоеточия – подходящие пары:
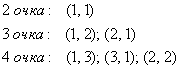
Итого: 6 благоприятствующих комбинаций.
Таким образом:
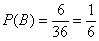 – вероятность того, что выпадет не более 4 очков. – вероятность того, что выпадет не более 4 очков.
в) Рассмотрим событие: 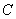 – выпадет от 3 до 9 очков включительно. Здесь можно пойти прямой дорогой, но… что-то не хочется. Да, некоторые пары уже перечислены в предыдущих пунктах, но работы все равно предстоит многовато. – выпадет от 3 до 9 очков включительно. Здесь можно пойти прямой дорогой, но… что-то не хочется. Да, некоторые пары уже перечислены в предыдущих пунктах, но работы все равно предстоит многовато.
Как лучше поступить?
В подобных случаях рациональным оказывается окольный путь. Рассмотрим противоположное событие: 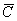 – выпадет 2 или 10 или 11 или 12 очков. – выпадет 2 или 10 или 11 или 12 очков.
В чём смысл? Противоположному событию благоприятствует значительно меньшее количество пар:

Итого: 7 благоприятствующих исходов.
По классическому определению:
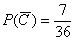 – вероятность того, что выпадет меньше трёх или больше 9 очков. – вероятность того, что выпадет меньше трёх или больше 9 очков.
Далее пользуемся тем, что сумма вероятностей противоположных событий равна единице:
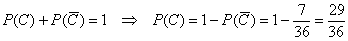 – вероятность того, что выпадет от 3 до 9 очков включительно. – вероятность того, что выпадет от 3 до 9 очков включительно.
Особо щепетильные люди могут перечислить все 29 пар, выполнив тем самым проверку.
Ответ: 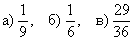
В следующей задаче повторим таблицу умножения:
Задача 21
Найти вероятность того, что при броске двух игральных костей произведение очков:
а) будет равно семи;
б) окажется не менее 20;
в) будет чётным.
Краткое решение и ответ в конце книги.
Помимо прямого перечисления и подсчёта исходов, в ходу также различные комбинаторные формулы. Эпичная задача про лифт:
Задача 22
В лифт 20-этажного дома на первом этаже зашли 3 человека. И поехали. Найти вероятность того, что:
а) они выйдут на разных этажах
б) двое выйдут на одном этаже;
в) все выйдут на одном этаже.
Решение: вычислим общее количество исходов: 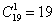 способами может выйти из лифта 1-й пассажир и способами может выйти из лифта 1-й пассажир и 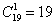 способами – 2-й пассажир и способами – 2-й пассажир и 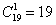 способами – третий пассажир. По правилу умножения комбинаций: способами – третий пассажир. По правилу умножения комбинаций: 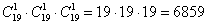 возможных исходов. То есть, каждый этаж выхода 1-го человека может комбинироваться с каждым этажом выхода 2-го человека и с каждым этажом выхода 3-го человека. возможных исходов. То есть, каждый этаж выхода 1-го человека может комбинироваться с каждым этажом выхода 2-го человека и с каждым этажом выхода 3-го человека.
Второй способ опять же основан на размещениях с повторениями:
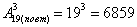 способами можно разместить пассажиров по трём этажам, причём этажи (два или все три) могут совпадать. способами можно разместить пассажиров по трём этажам, причём этажи (два или все три) могут совпадать.
Кому как понятнее, кому как удобнее.
а) Рассмотрим событие: 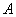 – пассажиры выйдут на разных этажах. В данном случае имеют место быть размещения: – пассажиры выйдут на разных этажах. В данном случае имеют место быть размещения:
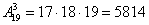 способами могут выйти 3 пассажира на разных этажах. способами могут выйти 3 пассажира на разных этажах.
Или так: 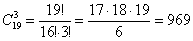 способами можно выбрать 3 этажа из 19 и способами можно выбрать 3 этажа из 19 и 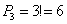 способами «переставить» пассажиров в каждом варианте. По правилу умножения комбинаций: способами «переставить» пассажиров в каждом варианте. По правилу умножения комбинаций: 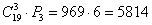 . .
По классическому определению вероятности:
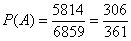
Теперь подумаем вот над какой вещью: пункт «бэ» достаточно сложен, и значительная часть читателей просто не справятся с этим пунктом. Но только не те, которые прочитают пару следующих абзацев!
в) Рассмотрим событие: 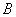 – пассажиры выйдут на одном этаже. Данному событию благоприятствуют – пассажиры выйдут на одном этаже. Данному событию благоприятствуют 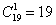 исходов и по классическому определению, соответствующая вероятность: исходов и по классическому определению, соответствующая вероятность: 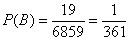 . .
Заходим с чёрного хода:
б) Рассмотрим событие: 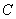 – два человека выйдут на одном этаже (и, соответственно, третий – на другом). – два человека выйдут на одном этаже (и, соответственно, третий – на другом).
События 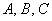 образуют полную группу (считаем, что в лифте никто не уснёт и лифт не застрянет =)), а значит, образуют полную группу (считаем, что в лифте никто не уснёт и лифт не застрянет =)), а значит, 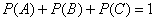 . .
В результате, искомая вероятность:
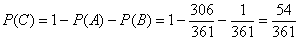
Таким образом, теорема о сложении вероятностей событий, образующих полную группу, может быть не только удобной, но и стать самой настоящей палочкой-выручалочкой!
Ответ: 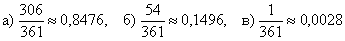
Когда получаются большие дроби, то хорошим тоном будет указать их приближенные десятичные значения. Обычно округляют до 2-4 знаков после запятой.
Поскольку события пунктов «а», «бэ», «вэ» образуют полную группу, то есть смысл выполнить контрольную проверку, причём лучше с приближенными значениями:
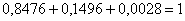 , что и требовалось проверить , что и требовалось проверить
Иногда по причине погрешности округлений может получиться 0,9999 либо 1,0001, в этом случае одно из приближенных значений следуют «подогнать» так, чтобы в сумме нарисовалась «чистая» единица.
Творческая задача для самостоятельного решения:
Задача 23
У Васи дома живут четыре кота, каждый из которых после завтрака случайным образом может выйти на прогулку или остаться дома. Какова вероятность того, что завтра после завтрака уйдут гулять 2 кота.
Да, авторы задачников, преподаватели любят придумывать свои задачи, и я не исключение. Цель благородна – заставить учащихся ДУМАТЬ и РАССУЖДАТЬ самостоятельно, а не пользоваться стандартными шаблонами.
Иногда в ходе рассуждений бывает просто необходимо что-нибудь почертить, что-нибудь порисовать, чтобы отыскать решение:
Задача 24
На семиместную скамейку случайным образом рассаживается 7 человек. Какова вероятность того, что два определённых человека окажутся рядом?
Решение: с общим количеством исходов проблем не возникает:
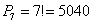 способами могут рассесться 7 человек на скамейке. способами могут рассесться 7 человек на скамейке.
Но вот как подсчитать количество благоприятствующих исходов? Тривиальные формулы не подходят и единственный путь – это логические рассуждения. Сначала рассмотрим ситуацию, когда Саша и Маша оказались рядом на левом краю скамейки:

Очевидно, что порядок имеет значение: слева может сидеть Саша, справа Маша и наоборот. Но это ещё не всё – для каждого из этих двух случаев остальные люди могут рассесться на свободных местах 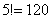 способами. Выражаясь комбинаторно, Сашу и Машу можно переставить на соседних местах способами. Выражаясь комбинаторно, Сашу и Машу можно переставить на соседних местах 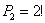 способами и для каждой перестановки других людей можно переставить способами и для каждой перестановки других людей можно переставить 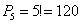 способами. способами.
Таким образом, по правилу умножения комбинаций, получается 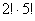 исходов. исходов.
Но и это ещё не всё! Перечисленные факты справедливы для каждой пары соседних мест:
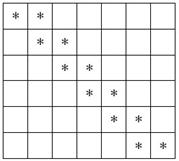
Интересно отметить, что если скамейку «скруглить» (соединяя левое и правое место), то получится дополнительная, седьмая пара соседних мест. Но не будем отвлекаться. Согласно тому же принципу умножения комбинаций, получаем окончательное количество благоприятствующих исходов: 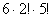
По классическому определению:
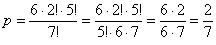 – вероятность того, что два определённых человека окажутся рядом. – вероятность того, что два определённых человека окажутся рядом.
Ответ: 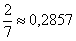
Не стесняйтесь снабжать трудные задачи рисунками или чертежами, поскольку «голые» словесные комментарии чреваты ошибками – если и не запутаетесь, то можете запросто обсчитаться.
И в заключительной части параграфа рассмотрим очень распространённый тип задач, который с высочайшей вероятностью встретится в вашем курсе:
Задача 25
Какова вероятность того, что в четырех сданных картах будет один туз и один король?
Решение: коль скоро неизвестный автор умолчал о колоде, будем считать, что в ней 36 карт. Ну а зачем нам больше? =)
Вычислим общее количество исходов. Сколькими способами можно извлечь 4 карты из колоды? Наверное, все поняли, что речь идёт о количестве сочетаний:
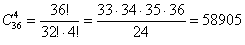 способами можно выбрать 4 карты из колоды. способами можно выбрать 4 карты из колоды.
Теперь считаем благоприятствующие исходы. По условию, в выборке из 4 карт должен быть один туз, один король и, о чём не сказано открытым текстом – две другие карты:
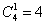 способами можно извлечь одного туза; способами можно извлечь одного туза;
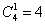 способами можно выбрать одного короля. способами можно выбрать одного короля.
Исключаем из рассмотрения тузов и королей:
36 – 4 – 4 = 28
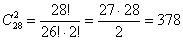 способами можно извлечь две другие карты. способами можно извлечь две другие карты.
По правилу умножения комбинаций:
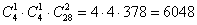 способами можно извлечь искомую комбинацию карт (1-го туза и 1-го короля и две другие карты). способами можно извлечь искомую комбинацию карт (1-го туза и 1-го короля и две другие карты).
Прокомментирую комбинационный смысл записи 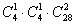 другим способом: другим способом:
каждый туз комбинируется с каждым королем и с каждой возможной парой других карт.
По классическому определению:
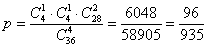 – вероятность того, что среди четырех сданных карт будет один туз и один король. – вероятность того, что среди четырех сданных карт будет один туз и один король.
Если хватает времени и терпения, максимально сокращайте большие дроби.
Ответ: 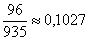
Стандартная задача для самостоятельного решения:
Задача 26
В ящике находится 15 качественных и 5 бракованных деталей. Наудачу извлекаются 2 детали. Найти вероятность того, что:
а) обе детали будут качественными;
б) одна деталь будет качественной, а одна – бракованной;
в) обе детали бракованны.
События перечисленных пунктов образуют полную группу, поэтому проверка здесь напрашивается сама собой.
И ещё одна задача, которая не только популярна, но и актуальна для многих читателей. Когда она мне попадается на глаза, то я всегда думаю: «чего же он так много выучил-то?!». Поэтому сделаю пример более реалистичным :=)
Задача 27
Студент знает ответы на 25 экзаменационных вопросов из 60. Какова вероятность сдать экзамен, если для этого необходимо ответить не менее чем на 2 из 3 вопросов?
Узнайте, насколько велики ваши шансы J И, конечно же, эти шансы нужно всячески увеличивать, едем дальше:
 1.5. Геометрическое определение вероятности 1.5. Геометрическое определение вероятности
 1.3.8. Размещения с повторениями 1.3.8. Размещения с повторениями
| Оглавление |
|

 Практикум по теории вероятностей
Практикум по теории вероятностей Научись решать в считанные дни!
Научись решать в считанные дни!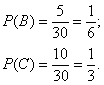
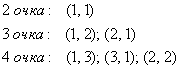


 1.5. Геометрическое определение вероятности
1.5. Геометрическое определение вероятности 1.3.8. Размещения с повторениями
1.3.8. Размещения с повторениями