2.2.8. Вероятность попадания в промежуток
Найдём 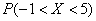 – вероятность того,
что случайная величина – вероятность того,
что случайная величина 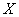 примет
какое-нибудь значение из интервала примет
какое-нибудь значение из интервала 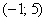 . .
В данном случае концы интервала (–1 и 5) находятся в области непрерывности функции распределения поэтому: 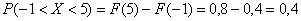 . .
И действительно, на данном интервале находятся значения 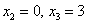 , вероятности появления которых: , вероятности появления которых: 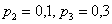 . .
Вычислим вероятность 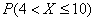 . Оба
конца этого промежутка не «попадают» в точки разрыва, поэтому: . Оба
конца этого промежутка не «попадают» в точки разрыва, поэтому:
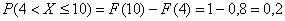 – вероятность того, что
случайная величина – вероятность того, что
случайная величина 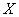 примет
значение из данного промежутка. И в самом деле – на нём находится единственное значение примет
значение из данного промежутка. И в самом деле – на нём находится единственное значение 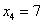 , которое может появиться с вероятностью , которое может появиться с вероятностью 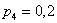 . .
Та же самая история с 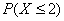 –
единственное, тут левый конец промежутка равен «минус» бесконечности: –
единственное, тут левый конец промежутка равен «минус» бесконечности:
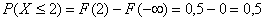 – самостоятельно
проанализируйте, какие значения – самостоятельно
проанализируйте, какие значения 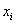 , и с какими вероятностями располагаются на промежутке , и с какими вероятностями располагаются на промежутке 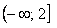
Теперь более занятная ситуация, где нужно особо включать голову: если хотя бы один из концов 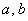 промежутка «попадает» в точку
разрыва функции промежутка «попадает» в точку
разрыва функции 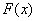 , то указанную
выше формулу можно использовать лишь в одном случае из четырёх, а именно для неравенства: , то указанную
выше формулу можно использовать лишь в одном случае из четырёх, а именно для неравенства:
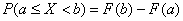
Примечание: если 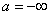 , то
левое неравенство становится строгим, но формула тоже применима. , то
левое неравенство становится строгим, но формула тоже применима.
Найдём 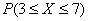 . Как быть? – под
правило не подходит! Вспоминаем теоремы тервера. По теореме сложения вероятностей несовместных событий: . Как быть? – под
правило не подходит! Вспоминаем теоремы тервера. По теореме сложения вероятностей несовместных событий:
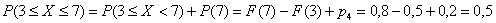 – вероятность того, что
случайная величина – вероятность того, что
случайная величина 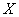 примет
значение из отрезка примет
значение из отрезка 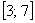 . .
И действительно, этот отрезок включает в себя два значения 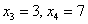 , которые появляются с вероятностями , которые появляются с вероятностями 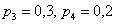 . .
Тут же рассмотрим три других неравенства:
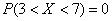 , т.к. на интервале , т.к. на интервале 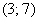 нет значений случайной величины.
Да-да, так и пишем. нет значений случайной величины.
Да-да, так и пишем.
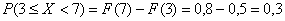 – это «штатный» случай
(см. правило). – это «штатный» случай
(см. правило).
И для 2-го полуинтервала используем теорему сложения вероятностей несовместных событий:
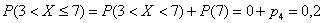
Едем дальше:
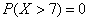 – поскольку там нет
значений случайной величины. – поскольку там нет
значений случайной величины.
Кстати, случай с нестрогим неравенством – есть «штатный» случай:
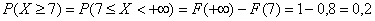 , который можно оформить и
так: , который можно оформить и
так:
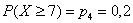 – ведь на функции
распределения «свет клином не сошёлся». – ведь на функции
распределения «свет клином не сошёлся».
И, наконец, типовая вероятность 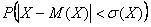 – того, что значение случайной величины – того, что значение случайной величины 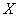 отклонится от своего математического ожидания не более чем на одно среднее квадратическое отклонение. И, как вы догадываетесь, эти характеристики нужно
вычислить. Но на самом деле не нужно, поскольку они уже рассчитаны в Задаче 87: отклонится от своего математического ожидания не более чем на одно среднее квадратическое отклонение. И, как вы догадываетесь, эти характеристики нужно
вычислить. Но на самом деле не нужно, поскольку они уже рассчитаны в Задаче 87:
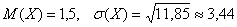
Раскрываем модуль:
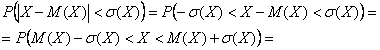
подставляем конкретные значения 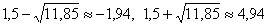 и пользуемся тем фактом, что они не «попадают» в точки разрыва функции
распределения: и пользуемся тем фактом, что они не «попадают» в точки разрыва функции
распределения:
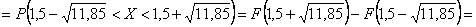 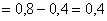 – искомая вероятность. – искомая вероятность.
Напоминаю, что в типичном случае на интервале 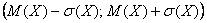 или вблизи него «сконцентрированы» наиболее вероятные значения случайной
величины. Так сказать, «центр событий». или вблизи него «сконцентрированы» наиболее вероятные значения случайной
величины. Так сказать, «центр событий».
Ответ:
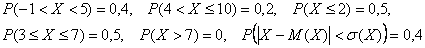
Аналогичное задание для самоконтроля, весь трафарет приведён выше:
Задача 94
Составить функцию распределения случайной величины 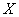

Выполнить чертёж. Найти вероятности следующих событий:

Подумайте над рациональным масштабом графика. Если возникают сомнению с нахождением вероятностей, помните – их всегда можно
пересчитать вручную, просто посмотрев на исходную табличку.
Решение и ответ там, где обычно.
И не успел я запостить этот материал на сайте (давно это было J), как от читателей стали поступать просьбы включить
в статью контрольный пример. Я даже прослезился (прямо как тот
профессор), и, конечно же, не смог вам отказать:
 2.2.9. Контрольное задание 2.2.9. Контрольное задание
 2.2.7. Функция распределения случайной величины 2.2.7. Функция распределения случайной величины
| Оглавление |
|

 Практикум по теории вероятностей
Практикум по теории вероятностей Научись решать в считанные дни!
Научись решать в считанные дни!

 2.2.9. Контрольное задание
2.2.9. Контрольное задание 2.2.7. Функция распределения случайной величины
2.2.7. Функция распределения случайной величины