2.2.7. Функция распределения случайной величины
Стандартное обозначение: 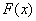
И для дискретной, и для непрерывной случайной величины она определяется одинаково:
Построим функцию распределения для нашей подопытной игры:
Начинаем разбираться. Чему, например, равно значение 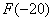 ? Это вероятность того, что выигрыш будет меньше, чем –20. И это невозможное событие: ? Это вероятность того, что выигрыш будет меньше, чем –20. И это невозможное событие: 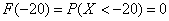 . Совершенно понятно, что . Совершенно понятно, что 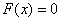 и для всех «икс» из интервала и для всех «икс» из интервала 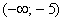 , а также для , а также для 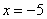 . Почему? По определению функции распределения: . Почему? По определению функции распределения:
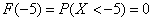 – вы согласны? Функция – вы согласны? Функция
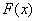 возвращает вероятность того,
что в точке возвращает вероятность того,
что в точке 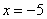 выигрыш
будет СТРОГО МЕНЬШЕ «минус» пяти. выигрыш
будет СТРОГО МЕНЬШЕ «минус» пяти.
Таким образом: 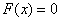 , если , если 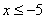 . .
На интервале 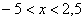 функция функция 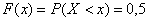 , поскольку левее
любой точки этого интервала есть только одно значение , поскольку левее
любой точки этого интервала есть только одно значение 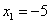 случайной величины, которое появляется с вероятностью 0,5. Кроме того,
сюда же следует отнести точку случайной величины, которое появляется с вероятностью 0,5. Кроме того,
сюда же следует отнести точку 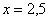 ,
так как: ,
так как:
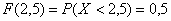 – очень хорошо осознайте этот
момент! – очень хорошо осознайте этот
момент!
Таким образом, если 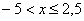 , то , то 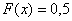
Далее рассматриваем промежуток 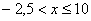 . СТРОГО ЛЕВЕЕ любой точки этого промежутка находятся два выигрыша . СТРОГО ЛЕВЕЕ любой точки этого промежутка находятся два выигрыша 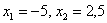 , поэтому: , поэтому:
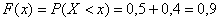
И, наконец, если 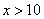 , то , то 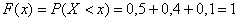 , ибо все значения , ибо все значения
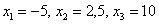 случайной величины случайной величины 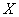 лежат СТРОГО левее
любой точки интервала лежат СТРОГО левее
любой точки интервала 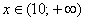
Заметим, кстати, важную особенность: коль скоро функция 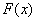 характеризует вероятность, то
она может принимать значения лишь из промежутка характеризует вероятность, то
она может принимать значения лишь из промежутка 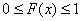 – и никакие другие! – и никакие другие!
Итак, функция распределения вероятностей ДСВ является кусочной и, как многие знают, в таких случаях принято использовать
фигурные скобки:
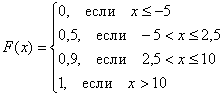
График данной функции имеет разрывный «ступенчатый» вид:
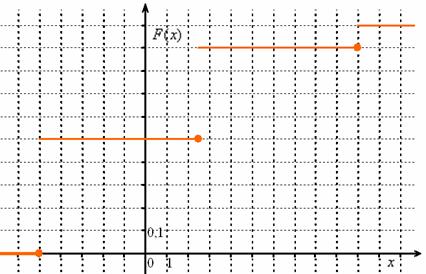
Причём, функция 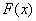 или её
график однозначно определяют сам закон распределения: в точке или её
график однозначно определяют сам закон распределения: в точке 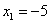 высота «ступеньки» (разрыв) составляет высота «ступеньки» (разрыв) составляет 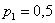 (следим по графику), в точке (следим по графику), в точке 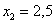 «скачок» разрыва равен «скачок» разрыва равен 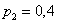 и, наконец, в точке и, наконец, в точке 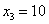 он равен в точности он равен в точности 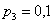 . .
Таким образом, функция распределения вероятностей – это ещё один способ ЗАДАТЬ случайную величину. И этот способ
особо важен для непрерывной случайной величины – по той причине, что её невозможно описать таблицей (ввиду бесконечного и
несчётного количества принимаемых значений). Однако, всему своё время, и НСВ – тоже.
Освоим технические моменты решения типовой задачи:
Задача 93
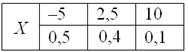
Построить функцию распределения случайной величины 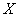
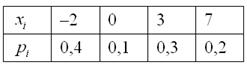
Найти вероятности того, что случайная величина примет значение из следующих промежутков:
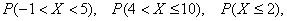
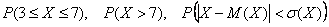 …, пожалуй, достаточно. …, пожалуй, достаточно.
Решение: На практике удобно использовать формальный алгоритм построения функции распределения:
Сначала берём первое значение 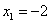 и составляем нестрогое неравенство и составляем нестрогое неравенство 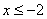 . На этом промежутке . На этом промежутке 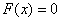 . .
На промежутке 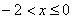 (между (между
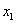 и и 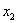 ): ):
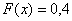
На промежутке 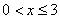 (между (между
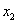 и и 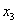 ): ):
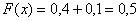
На промежутке 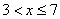 (между (между
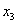 и и 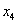 ): ):
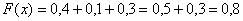
И, наконец, если 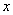 строго
больше самого последнего значения строго
больше самого последнего значения 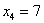 , то: , то:
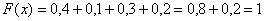
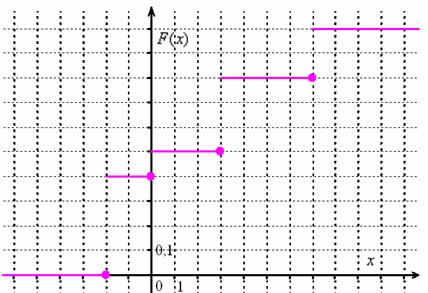
Легко заметить, что с увеличением «икс» идёт накопление (суммирование) вероятностей, и поэтому функцию 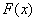 иногда называют интегральной функцией распределения. В
практических задачах проведённые выше действия обычно выполняют устно, а результат сразу записывают под единую скобку: иногда называют интегральной функцией распределения. В
практических задачах проведённые выше действия обычно выполняют устно, а результат сразу записывают под единую скобку:

Выполним чертёж:
и проконтролируем правильность решения с помощью «скачков» графика: в точке 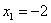 «скачок» равен «скачок» равен 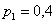 , в точке , в точке 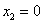 составляет составляет 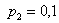 , в точке , в точке 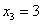 равен равен 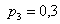 , и, наконец, в точке , и, наконец, в точке 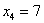 – – 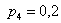 . .
При выполнении чертежа от руки оптимален следующий масштаб:
горизонтальная ось: 1 ед. = 2 или 1 тетрадная клетка;
вертикальная ось: 0,1 = 1 тетрадная клетка.
На левых концах ступенек (кроме нижнего луча) можно ставить выколотые точки – дело вкуса. Левый нижний луч следует прочертить жирно
(чтобы он не сливался с координатной осью) и до конца оси! Правая верхняя линия не должна заканчиваться раньше
острия оси! Такие оплошности могут говорить о непонимании функции распределения, а это, как вы понимаете, скверно. То было ручное
построение. Ну а о том, как строить такие красивые графики в Экселе можно узнать в этом ролике на Ютубе, к слову, полигон (многоугольник) распределения строится ещё проще.
Переходим ко второй части задания, её коротко можно сформулировать так:
 2.2.8. Вероятность попадания в промежуток 2.2.8. Вероятность попадания в промежуток
 2.2.6. Многоугольник распределения 2.2.6. Многоугольник распределения
|

 Практикум по теории вероятностей
Практикум по теории вероятностей Научись решать в считанные дни!
Научись решать в считанные дни!
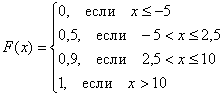




 2.2.8. Вероятность попадания в промежуток
2.2.8. Вероятность попадания в промежуток 2.2.6. Многоугольник распределения
2.2.6. Многоугольник распределения