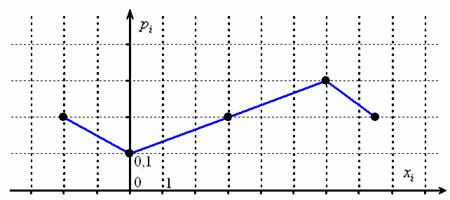
2.2.6. Многоугольник распределения

Итак, пусть дискретная случайная величина задана своим законом распределения:

Многоугольником распределения вероятностей данной величины называют ломаную, звенья которой соединяют соседние точки . Иногда вместо «многоугольника» используют термин полигон, но этот вариант больше в ходу в математической статистике.

Всё очень просто:

Задача 91
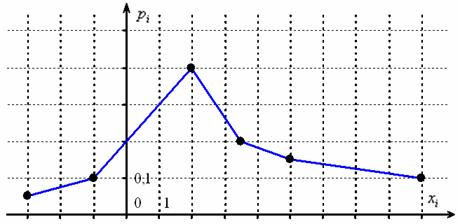
Построить многоугольник распределения вероятностей случайной величины

Решение: чертим прямоугольную систему координат, в которой по оси абсцисс отсчитываются – значения случайной величины, а по оси ординат – их вероятности. Отмечаем на чертеже точки , в данном случае их пять, и соединяем «соседей» отрезками:

При выполнении чертежа от руки по возможности придерживайтесь следующего масштаба:
горизонтальная ось: 1 ед. = 2 тетрадные клетки (1 см);
вертикальная ось: 0,1 = 2 тетрадные клетки.

Если значения достаточно велики, то ось абсцисс можно «разорвать» (не чертить её кусочек после единицы), и справа продолжить нумерацию, например, с 20.

Теперь обратите внимание на следующую важную вещь: помимо того, что дискретную случайную величину можно изобразить с помощью многоугольника – её ведь можно ещё и ЗАДАТЬ этим способом. До сих пор мы делали это с помощью таблички, но никто же не мешает использовать и чертёж!

Задача 92
Дискретная случайная величина задана своим многоугольником

Записать закон распределения данной случайной величины, выполнить проверку.

Это задание для самостоятельного решения. И тут мы, кстати, видим изъян графического способа: по чертежу не всегда понятны точные значения случайной величины и их вероятности.

На практике задачи с многоугольником встречаются довольно часто, но гораздо бОльшее распространение получила:

2.2.7. Функция распределения случайной величины

2.2.5. Формула для вычисления дисперсии

| Оглавление |