Ваш репетитор, справочник и друг!

Практикум по теории вероятностей

Научись решать в считанные дни!

2.2.5. Формула для вычисления дисперсии

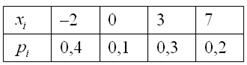
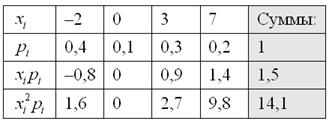
Данная формула выводится непосредственно из определения дисперсии, и мы незамедлительно пускаем её в оборот. Скопирую сверху табличку с нашей игрой:

и найденное матожидание .

Вычислим дисперсию вторым способом. Сначала найдём математическое ожидание – квадрата случайной величины . По определению математического ожидания, значения случайной величины следует перемножить на соответствующие вероятности и эти произведения сложить:

в данном случае:

Таким образом, по формуле:

Как говорится, почувствуйте разницу. И на практике, конечно, лучше применять формулу (если иного не требует условие).

Осваиваем технику решения и оформления:

Задача 87
Дискретная случайная величина задана своим законом распределения:

Найти её математическое ожидание, дисперсию и среднее квадратическое отклонение.

Эта задача встречается повсеместно, и, как правило, идёт без содержательного смысла. Но желающие могут представить четыре лампочки с числами, которые загораются в дурдоме с определёнными вероятностями :)

Решение: Основные вычисления удобно свести в таблицу. Сначала в верхние две строки записываем исходные данные. Затем рассчитываем произведения , затем и, наконец, суммы в правом столбце:

Собственно, почти всё готово. В третьей строке нарисовалось готовенькое математическое ожидание: .

Дисперсию вычислим по формуле:

И, наконец, среднее квадратическое отклонение:
– лично я обычно округляю результат до 2 знаков после запятой.

Все вычисления можно провести на калькуляторе, а ещё лучше – в Экселе (ссылка на видеоролик на Ютубе). Вот здесь вот уже будет трудно ошибиться.

Ответ:

Пара заданий для самостоятельного решения:

Задача 88
Вычислить дисперсию случайной величины предыдущего примера по определению.

…встречается и такая задача, я ничего не придумываю. Почти J

И аналогичный пример:

Задача 89
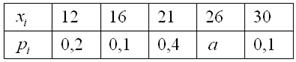
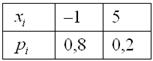
Дискретная случайная величина задана своим законом распределения:

Найти

Да, значения случайной величины бывают достаточно большими, и здесь по возможности лучше использовать Эксель.

И в заключение параграфа разберём ещё одну типовую задачу, можно даже сказать, небольшой ребус:

Задача 90
Дискретная случайная величина может принимать только два значения: и , причём . Известна вероятность , математическое ожидание и дисперсия .

Найти .

Решение: начнём с неизвестной вероятности. Так как случайная величина может принять только два значения, то сумма вероятностей соответствующих событий:

и поскольку , то .

Осталось найти …, легко сказать :) Но да ладно, понеслось. По определению математического ожидания:
– подставляем известные величины:

– и больше из этого уравнения ничего не выжать, разве что можно переписать его в привычном направлении:

ОК, едем дальше. По формуле вычисления дисперсии:
– подставляем известные данные:

и реверанс:
О дальнейших действиях, думаю, вы догадываетесь. Составим и решим систему:

Десятичные дроби – это, конечно, безобразие, умножаем оба уравнения на 5:

Вот так-то лучше. Из 1-го уравнения выражаем:
(это более простой путь) – подставляем во 2-е уравнение:

Возводим разность в квадрат и проводим упрощения:

В результате получено квадратное уравнение, находим его дискриминант:
и извлекаем из него корень:
– отлично, целое значение, значит, мы на верном пути.

Таким образом, у нас получаются два решения:

1) если , то ;

2) если , то .

Условию удовлетворяет первая пара корней. С высокой вероятностью всё правильно, но, тем не менее, запишем закон распределения:

и выполним проверку, а именно, найдём матожидание:

и дисперсию:

В результате получены исходные значения, что и требовалось проверить.

Ответ: …да, вроде бы такие простенькие числа, но вычисления…, и поэтому в этой задаче следует проявлять повышенное внимание.

Переходим к графическому представлению дискретной случайной величины:

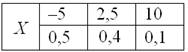
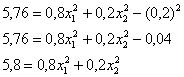
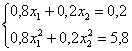
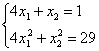
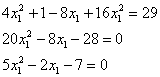
2.2.6. Многоугольник распределения

2.2.4. Среднее квадратическое отклонение

| Оглавление |

Полную и свежую версию этой книги в pdf-формате,
а также курсы по другим темам можно найти после Оглавления.

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!

С наилучшими пожеланиями, Александр Емелин