|
Ваш репетитор, справочник и друг!
|
1.1.1. ПодмножестваПрактически всё понятно из самого названия: множество Согласно определению, любое множество можно считать подмножеством самого себя: Вернёмся к примеру, где Также можно выделить подмножество согласных букв и вообще – произвольное подмножество, состоящее из любого количества случайно (или неслучайно) взятых букв. В частности, любая выбранная буква является подмножеством множества «Тривиальный», в переводе на молодёжный язык – это беспонтовый :) Отношения между множеством и подмножествами удобно изображать с помощью условной геометрической схемы, которая называется кругами Эйлера. Пусть Типичный пример включений мы наблюдаем при рассмотрении числовых множеств. Ещё раз повторим школьный материал: |
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Высшая алгебра для начинающих
Высшая алгебра для начинающих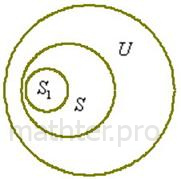
 1.1.2. Числовые множества
1.1.2. Числовые множества 1.1. Множества
1.1. Множества