1.1.2. Числовые множества
Как известно, сначала люди освоили натуральные числа – для подсчёта материальных объектов (людей, коней, овец, монет и т.д.). Это множество уже встретились выше, единственное, мы сейчас чуть-чуть модифицируем его обозначение. Дело в том, что числовые множества принято обозначать жирными, стилизованными или утолщёнными буквами. Мне удобнее использовать жирный шрифт:
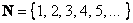 , иногда к множеству натуральных чисел относят ноль. , иногда к множеству натуральных чисел относят ноль.
Если к множеству 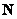 присоединить те же числа с противоположным знаком и ноль, то получится множество целых чисел: присоединить те же числа с противоположным знаком и ноль, то получится множество целых чисел:
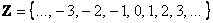 , рационализаторы и лентяи любят использовать значки «плюс минус»: , рационализаторы и лентяи любят использовать значки «плюс минус»:
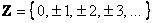
Совершенно понятно, что множество натуральных чисел является подмножеством множества целых чисел:
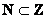 – по той причине, что каждый элемент множества – по той причине, что каждый элемент множества 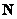 принадлежит множеству принадлежит множеству 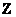 . Таким образом, любое натуральное число можно смело назвать и целым числом. . Таким образом, любое натуральное число можно смело назвать и целым числом.
Следующим числовым множеством идёт множество рациональных чисел:
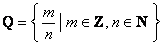 – то есть, любое рациональное число представимо в виде дроби – то есть, любое рациональное число представимо в виде дроби 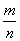 с целым числителем и натуральным знаменателем. с целым числителем и натуральным знаменателем.
Очевидно, что множество целых чисел является подмножеством множества рациональных чисел:
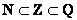
И в самом деле – любое целое число можно представить в виде рациональной дроби 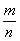 , например: , например: 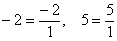 и т. д. Таким образом, целое число можно совершенно «законно» назвать и рациональным числом. и т. д. Таким образом, целое число можно совершенно «законно» назвать и рациональным числом.
Характерным «опознавательным» признаком рационального числа является то обстоятельство, что при делении числителя на знаменатель получается либо
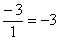 – целое число, либо – целое число, либо
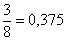 – конечная десятичная дробь, либо бесконечная периодическая десятичная дробь: – конечная десятичная дробь, либо бесконечная периодическая десятичная дробь:
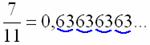
(повтор может начаться не сразу).
И важнейшая мантра:
В высшей математике все действия стремимся выполнять
в обыкновенных (правильных и неправильных) дробях.
Согласитесь, что иметь дело с дробью 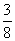 значительно удобнее, чем с десятичным числом 0,375 (не говоря уже о бесконечных дробях). значительно удобнее, чем с десятичным числом 0,375 (не говоря уже о бесконечных дробях).
Едем дальше. Помимо рациональных, существует множество 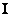 иррациональных чисел, каждое из которых представимо в виде бесконечной НЕпериодической десятичной дроби. Иными словами, в «бесконечных хвостах» иррациональных чисел нет никакой закономерности: иррациональных чисел, каждое из которых представимо в виде бесконечной НЕпериодической десятичной дроби. Иными словами, в «бесконечных хвостах» иррациональных чисел нет никакой закономерности:
 («год рождения Льва Толстого» дважды) («год рождения Льва Толстого» дважды)
и т. д.
О знаменитых константах «пи» и «е» информации предостаточно, поэтому на них я не останавливаюсь.
Объединение рациональных и иррациональных чисел образует множество действительных (вещественных) чисел:
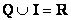
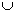 – значок объединения множеств. – значок объединения множеств.
Геометрическая интерпретация множества 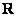 вам хорошо знакома – это числовая прямая: вам хорошо знакома – это числовая прямая:

Каждому действительному числу соответствует определённая точка числовой прямой, и наоборот – каждой точке числовой прямой обязательно соответствует некоторое действительное число. Это есть свойство непрерывности действительных чисел, которое хоть и кажется очевидным, но строго доказывается в курсе математического анализа
Числовую прямую также обозначают бесконечным интервалом 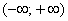 , а запись , а запись 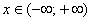 или эквивалентная ей запись или эквивалентная ей запись  символизирует тот факт, что символизирует тот факт, что 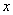 принадлежит множеству действительных чисел (или попросту «икс» – действительное число). принадлежит множеству действительных чисел (или попросту «икс» – действительное число).
С вложениями всё прозрачно: множество рациональных чисел – это подмножество множества действительных чисел:
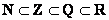 , таким образом, числа всех «предыдущих» множеств можно смело назвать и действительными числами. , таким образом, числа всех «предыдущих» множеств можно смело назвать и действительными числами.
Множество иррациональных чисел – это тоже подмножество действительных чисел: 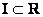
При этом подмножества 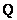 и и 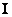 не пересекаются – то есть ни одно иррациональное число невозможно представить в виде рациональной дроби не пересекаются – то есть ни одно иррациональное число невозможно представить в виде рациональной дроби 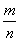 . .
Существуют ли какие-нибудь другие числовые множества? Существуют! Это, например, комплексные числа, с которыми мы ознакомимся буквально в ближайшие часы.
 1.1.3. Мощность множества 1.1.3. Мощность множества
 1.1.1. Подмножества 1.1.1. Подмножества
| Оглавление |
|

 Высшая алгебра для начинающих
Высшая алгебра для начинающих («год рождения Льва Толстого» дважды)
(«год рождения Льва Толстого» дважды)
 1.1.3. Мощность множества
1.1.3. Мощность множества 1.1.1. Подмножества
1.1.1. Подмножества