1.1.4. Операции (действия) с множествами
1) Пересечение множеств характеризуется логической связкой И (разберём чуть позже) и обозначается значком 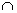 . .
Пересечением множеств 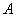 и и 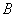 называется множество называется множество 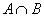 , каждый элемент которого принадлежит и множеству , каждый элемент которого принадлежит и множеству 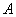 и множеству и множеству 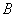 . Проще говоря, пересечение – это общая часть множеств: . Проще говоря, пересечение – это общая часть множеств:
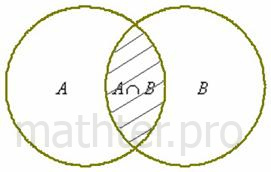
Схематическое изображение операции с множеством называется диаграммой Венна и перед вами одна из них.
Так, пересечение множеств 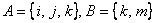 – есть множество: – есть множество: 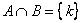
Если у множеств нет одинаковых элементов, то их пересечение пусто. Такой пример нам только что встретился при рассмотрении числовых множеств:
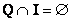 , при этом множества рациональных и иррациональных чисел можно схематически изобразить двумя непересекающимися кругами. , при этом множества рациональных и иррациональных чисел можно схематически изобразить двумя непересекающимися кругами.
Операция пересечения применима и для бОльшего количества множеств, например, для трёх. Обозначим через 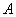 – множество заглавных букв русского алфавита, – множество заглавных букв русского алфавита, 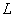 – множество заглавных букв латинского алфавита и – множество заглавных букв латинского алфавита и 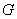 – множество больших букв греческого алфавита. Пересечение этих множеств – есть множество: – множество больших букв греческого алфавита. Пересечение этих множеств – есть множество:
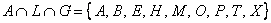 – элементы сего множества принадлежат и множеству – элементы сего множества принадлежат и множеству 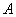 , и множеству , и множеству 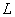 , и множеству , и множеству 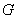 . .
…Какое-то получилось страшилище «АВЕНМОРТХ» :), но это я не ради шутки. Элементы множества желательно располагать в порядке их возрастания (если это возможно). Так мне легче будет проверять ваши решения ;) Следующая операция:
2) Объединение множеств характеризуется логической связкой ИЛИ и обозначается значком 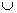
Объединением множеств 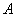 и и 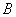 называется множество называется множество 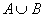 , каждый элемент которого принадлежит множеству , каждый элемент которого принадлежит множеству 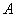 или множеству или множеству 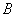 : :
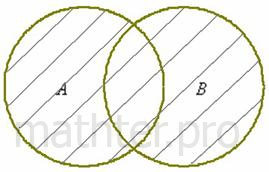
Запишем объединение множеств 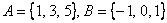 : :
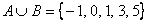 – тут нужно перечислить все элементы множеств – тут нужно перечислить все элементы множеств 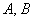 , причём одинаковые элементы (единицу на пересечении множеств) следует указать один раз. , причём одинаковые элементы (единицу на пересечении множеств) следует указать один раз.
Но множества, разумеется, могут и не пересекаться, как это имеет место быть с рациональными и иррациональными числами: 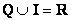 . В этом случае можно изобразить два непересекающихся заштрихованных круга. . В этом случае можно изобразить два непересекающихся заштрихованных круга.
Операция объединения применима и для бОльшего количества множеств, например, если 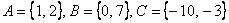 , то: , то:
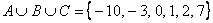 , просто и со вкусом. , просто и со вкусом.
3) Разностью множеств 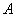 и и 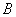 называют множество называют множество 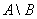 , каждый элемент которого принадлежит множеству , каждый элемент которого принадлежит множеству 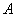 и не принадлежит множеству и не принадлежит множеству 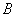 : :
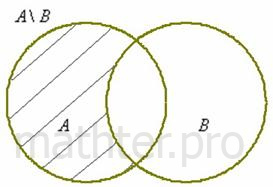
Разность 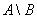 читаются следующим образом: «а без бэ». И рассуждать можно точно так же: рассмотрим множества читаются следующим образом: «а без бэ». И рассуждать можно точно так же: рассмотрим множества 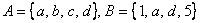 . Чтобы записать разность . Чтобы записать разность 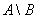 , нужно из множества , нужно из множества 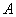 «выбросить» все элементы, которые есть во множестве «выбросить» все элементы, которые есть во множестве 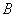 : :
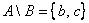
Пример с числовыми множествами:
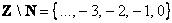 – здесь из множества целых чисел исключены все натуральные, да и сама запись – здесь из множества целых чисел исключены все натуральные, да и сама запись 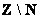 так и читается: «множество целых чисел без множества натуральных». так и читается: «множество целых чисел без множества натуральных».
Зеркально: разностью множеств 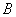 и и 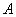 называют множество называют множество 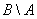 , каждый элемент которого принадлежит множеству , каждый элемент которого принадлежит множеству 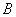 и не принадлежит множеству и не принадлежит множеству 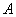 : :
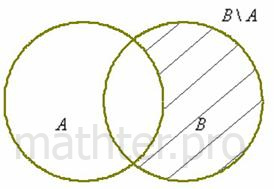
Для тех же множеств 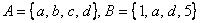
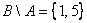 – из множества – из множества 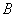 «выброшено» то, что есть во множестве «выброшено» то, что есть во множестве 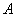 . .
А вот эта разность оказывается пуста: 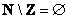 . И в самом деле – если из множества натуральных чисел исключить целые числа, то, собственно, ничего и не останется :) . И в самом деле – если из множества натуральных чисел исключить целые числа, то, собственно, ничего и не останется :)
Кроме того, иногда рассматривают симметрическую разность 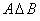 , которая объединяет оба «полумесяца»: , которая объединяет оба «полумесяца»:
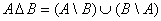 – иными словами, это «всё, кроме пересечения множеств». Диаграмму Венна изобразите самостоятельно. – иными словами, это «всё, кроме пересечения множеств». Диаграмму Венна изобразите самостоятельно.
4) Декартовым (прямым) произведением множеств 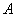 и и 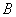 называется множество называется множество 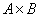 всех упорядоченных пар всех упорядоченных пар 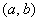 , в которых элемент , в которых элемент 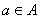 , а элемент , а элемент 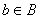 . .
Слово «упорядоченных» означает, что элемент, находящийся на первом месте 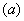 обязательно принадлежит множеству обязательно принадлежит множеству 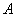 , а второй элемент , а второй элемент 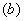 – строго множеству – строго множеству 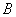 . .
Запишем декартово произведение множеств 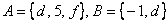 : :
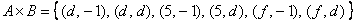 – перечисление пар удобно осуществлять по следующему алгоритму: «сначала к 1-му элементу множества – перечисление пар удобно осуществлять по следующему алгоритму: «сначала к 1-му элементу множества 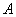 последовательно присоединяем каждый элемент множества последовательно присоединяем каждый элемент множества 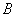 , затем ко 2-му элементу множества , затем ко 2-му элементу множества 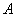 присоединяем каждый элемент множества присоединяем каждый элемент множества 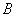 , и, наконец, к 3-му элементу множества , и, наконец, к 3-му элементу множества 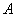 присоединяем каждый элемент множества присоединяем каждый элемент множества 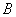 »: »:
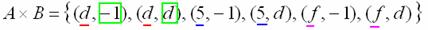
Зеркально: декартовым произведением множеств 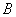 и и 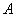 называется множество называется множество 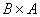 всех упорядоченных пар всех упорядоченных пар 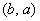 , в которых , в которых 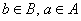 . В нашем примере: . В нашем примере:
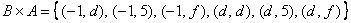 – здесь схема записи аналогична: сначала к «минус единице» последовательно присоединяем все элементы множества «а большое» и затем к «дэ» – те же самые элементы: – здесь схема записи аналогична: сначала к «минус единице» последовательно присоединяем все элементы множества «а большое» и затем к «дэ» – те же самые элементы:
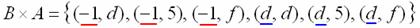
И гвоздь программы: декартово произведение 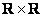 – есть не что иное, как множество точек – есть не что иное, как множество точек 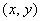 нашей родной декартовой системы координат нашей родной декартовой системы координат 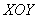 . …Все помнят такую? …Её забыть трудно. Но некоторые умудряются! . …Все помнят такую? …Её забыть трудно. Но некоторые умудряются!
А теперь пришла пора поразмяться вам, а то Вольдемар уже задремал на задней парте :) Задание для закрепления материала:
Задача 1
1) Записать все подмножества множества 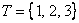
2) Является ли пустое множество подмножеством пустого множества?
3) Выполнить операции 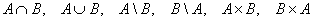 , если: , если:
а) 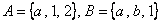 ; ;
б) 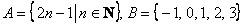
и пунктик с промежутками действительных чисел:
с) 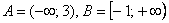 . .
Напоминаю, что квадратная скобка означает включение числа в промежуток, а круглая – его невключение, то есть «минус единица» принадлежит множеству 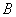 , а «тройка» не принадлежит множеству , а «тройка» не принадлежит множеству 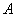 . Постарайтесь разобраться, что представляет собой декартово произведение данных множеств. Если появится туман, выполните чертёж ;) . Постарайтесь разобраться, что представляет собой декартово произведение данных множеств. Если появится туман, выполните чертёж ;)
Решаем самостоятельно!
Проверю всех!
Образец для сверки в конце книги
 1.1.5. Отображение множеств 1.1.5. Отображение множеств
 1.1.3. Мощность множества 1.1.3. Мощность множества
| Оглавление |
|

 Высшая алгебра для начинающих
Высшая алгебра для начинающих



 1.1.5. Отображение множеств
1.1.5. Отображение множеств 1.1.3. Мощность множества
1.1.3. Мощность множества