Ваш репетитор, справочник и друг!

Высшая алгебра для начинающих

1.1.5. Отображение множеств

Отображение множества во множество – это правило (закон), по которому каждому элементу множества ставится в соответствие элемент (или элементы) множества .

Множество называют образом отображения, а – прообразом.

Если в соответствие ставится единственный элемент, то данное правило называется однозначно определённой функцией или просто функцией. Функцию, как многие помнят, чаще всего обозначают буквой – она ставит в соответствие каждому элементу единственное значение , принадлежащее множеству .

Ну а сейчас я снова побеспокою множество студентов 1-го ряда
и предложу им шесть тем для рефератов (множество ), например, по такому правилу :

Установленный закон ставит в соответствие каждому студенту множества единственную тему реферата множества . Величина считается независимой переменной и называется аргументом функции, в данном случае она может принимать лишь 6 значений. Величина – есть зависимая переменная (от аргумента по закону ) и её называют значением функции.

Множество (прообраз) называют областью определения функции и обозначают через , а множество (образ отображения) – областью значений функции .

И, конечно, вы можете выбрать темы для рефератов самостоятельно, в этом случае получится другая (скорее всего) функция , которая каждому студенту множества поставит в соответствие желаемую тему из множества по правилу .

Построенное в этом примере отображение множеств имеет очень важную характеристику: оно является взаимно однозначным или биективным (биекцией). Это означает, что каждому студенту поставлена в соответствие одна уникальная тема реферата, и обратно – за каждой темой реферата закреплён один и только один студент.

Но, разумеется, не всякое отображение биективно. Так, если на 1-й ряд (к множеству ) добавить 7-го студента, то отображение перестанет быть взаимно однозначным – либо один из студентов останется без темы (не «отобразится» вообще), либо какая-то тема достанется сразу двум студентам. Обратная ситуация: если к множеству добавить
7-ю тему, то взаимная однозначность отображения тоже будет утрачена – одна из тем останется невостребованной.

…Уважаемые студенты 1-го ряда, не расстраивайтесь! – остальные после пар пойдут прибирать территорию университета от осенней листвы. Завхоз установит взаимно однозначное соответствие между ними и мётлами, а Вольдемар ещё и в магазин сбегать успеет! …И вот, кстати, вы знаете, чем хороший студент отличается от плохого? Хороший давно бы сбЕгал.

Теперь разберёмся со «школьной» функцией одной переменной . Возьмём простенький пример и задумаемся, что это такое? …Это правило , которое каждому действительному значению ставит в соответствие единственное значение . Проще говоря, эта функция удваивает действительные числа. Изобразим её график:

Так как «икс» может принимать любое действительное значение, то область определения функции: . И, в силу правила , «игрек», очевидно, тоже может быть любым действительным числом, таким образом, область значений функции: .

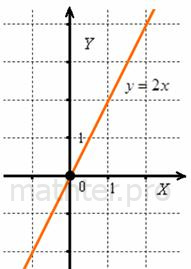
С теоретико-множественной точки зрения, здесь имеет место отображение множества действительных чисел во множество действительных чисел:

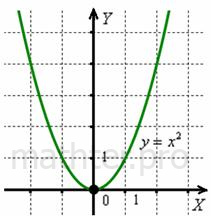
Первое множество мы по-обывательски называем «иксами» (независимая переменная или аргумент), а второе – «игреками» (зависимая переменная или функция).

Теперь взглянем на старую знакомую параболу :

Что делает эта функция? Здесь правило каждому значению ставит в соответствие его квадрат.

Аргумент может принять любое действительное значение, поэтому область определения: .

А вот с «игреком» всё занятнее: поскольку квадрат любого действительного числа неотрицателен, то область значений такова: .

Таким образом, имеет место отображение:

Итак, что же такое функция одной переменной? Функция одной переменной – это правило , которое каждому значению независимой переменной области определения ставит в соответствие одно и только одно значение .

Как уже отмечалось в примере со студентами, не всякая функция является взаимно-однозначной. Так, у функции каждому «иксу» области определения соответствует свой уникальный «игрек», и, наоборот – по любому значению «игрек» мы сможем однозначно восстановить «икс». Таким образом, это биективная функция.

А вот у квадратичной функции не наблюдается ничего подобного, во-первых:
– то есть, различные значения «икс» отобразились в одно и то же значение «игрек»; и во-вторых, если кто-то вычислил значение функции и сообщил нам, что , то не понятно – этот «игрек» получен при или при ? Что и говорить, взаимной однозначностью здесь даже не пахнет.

И самое время освежить в памяти основные элементарные функции:

Задача 2

Пользуясь Приложением К задаче 2, записать область определения и область значений каждой функции, а также указать, биективна она или нет.

С точки зрения грубой визуализации, область определения – это те значения «икс», где есть график функции. И область значений – это те «игреки», где график есть. Решаем самостоятельно, сверяемся (конец книги), и тема получает логичное продолжение:

1.1.6. Обратное отображение

1.1.4. Операции (действия) с множествами

| Оглавление |

Автор: Aлeксaндр Eмeлин