1.1.6. Обратное отображение
Прямое отображение 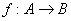 обратимо обратимо 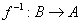 тогда и только тогда, когда оно взаимно однозначно. Откуда
следует, что тогда и только тогда, когда оно взаимно однозначно. Откуда
следует, что 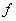 – это биективная функция, которые вы только что отлавливали в Задаче 2. – это биективная функция, которые вы только что отлавливали в Задаче 2.
На уровне обывательского понимания обратимость означает возможность «всё вернуть в исходное состояние», причём, идеально и
однозначно.
Так, если вы умножаем число «икс» на два: 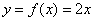 , то всегда
можно взять «игрек», разделить его пополам и получить исходное число: , то всегда
можно взять «игрек», разделить его пополам и получить исходное число: 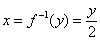 . .
Обратная к 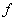 функция обозначается через функция обозначается через 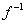 , но на практике с надстрочным индексом часто не заморачиваются и
просто пишут , но на практике с надстрочным индексом часто не заморачиваются и
просто пишут 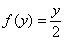 . И даже букву меняют, называя функции . И даже букву меняют, называя функции 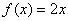 , , 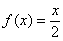 обратными, что не совсем, конечно, корректно. обратными, что не совсем, конечно, корректно.
Пример не обратимой функции тоже только что был: 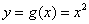 . Так, если нам предъявить значение . Так, если нам предъявить значение 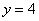 , то не понятно, то ли «икс» равнялся двум, то ли минус двум. Однако параболу можно
рассмотреть в кусочном виде: , то не понятно, то ли «икс» равнялся двум, то ли минус двум. Однако параболу можно
рассмотреть в кусочном виде:
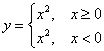 и каждый кусок в отдельности обратим: и каждый кусок в отдельности обратим:
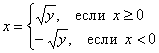
И это вполне себе обычная история.
 1.1.7. Композиция отображений 1.1.7. Композиция отображений
 1.1.5. Отображение множеств 1.1.5. Отображение множеств
| Оглавление |
|

 Высшая алгебра для начинающих
Высшая алгебра для начинающих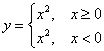 и каждый кусок в отдельности обратим:
и каждый кусок в отдельности обратим: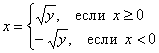
 1.1.7. Композиция отображений
1.1.7. Композиция отображений 1.1.5. Отображение множеств
1.1.5. Отображение множеств