1.1.7. Композиция отображений
Нет, это не композиции Моцарта или Чайковского :) А более общий случай – речь идёт о композиции действий: взяли глину и
вылепили горшок, затем взяли горшок и обожгли его печи. Действие – результат, действие над результатом – результат.
Композицией отображений 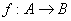 и и 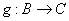 называется
отображение называется
отображение 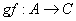 , которое каждому элементу , которое каждому элементу 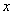 множества множества 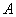 ставит в соответствие элемент (либо элементы) ставит в соответствие элемент (либо элементы) 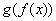 множества множества 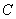 . .
Обратите внимание, что отображения 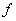 и и 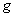 не обязаны быть однозначно
определёнными функциями, тем более взаимно однозначными. не обязаны быть однозначно
определёнными функциями, тем более взаимно однозначными.
Вернёмся к функции 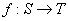 , которая каждому студенту из
множества , которая каждому студенту из
множества 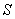 ставит в соответствие свою тему реферата из
множества ставит в соответствие свою тему реферата из
множества 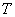 . Эта функция, и она биективна. Преподаватель
проверил работы и поставил в соответствие каждому реферату . Эта функция, и она биективна. Преподаватель
проверил работы и поставил в соответствие каждому реферату 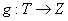 оценку из множества оценку из множества 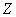 . Это тоже функция, но уже не взаимно однозначная, поскольку одной и той же оценке может
соответствовать несколько рефератов. . Это тоже функция, но уже не взаимно однозначная, поскольку одной и той же оценке может
соответствовать несколько рефератов.
Композиционное преобразование 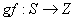 ставит в соответствие каждому
студенту оценку за реферат. В функциональном «школьном» стиле это запишется так: ставит в соответствие каждому
студенту оценку за реферат. В функциональном «школьном» стиле это запишется так: 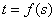 и и 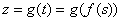 . .
Если же обе функции 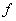 и и 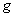 биективны,
то их композиция биективны,
то их композиция 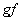 – тоже
биекция. – тоже
биекция.
К примеру, увеличим «икс» на три 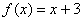 , а затем возведём число «е» в эту степень: , а затем возведём число «е» в эту степень: 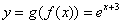 – в результате получена взаимно однозначная функция, поскольку функции – в результате получена взаимно однозначная функция, поскольку функции 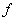 и и 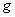 , очевидно, биективны. Более того, композиция биективных функций обратима: всегда и однозначно можно выяснить исходное значение «икс»: , очевидно, биективны. Более того, композиция биективных функций обратима: всегда и однозначно можно выяснить исходное значение «икс»: 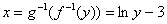 . .
И другой важный факт: в общем случае композиция не перестановочна 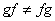 . Так, если «икс» сначала возвести в квадрат, а затем найти синус, то получится функция . Так, если «икс» сначала возвести в квадрат, а затем найти синус, то получится функция 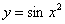 . Если же сначала найти синус икс, а затем возвести результат
в квадрат, то получится другая функция: . Если же сначала найти синус икс, а затем возвести результат
в квадрат, то получится другая функция: 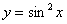 . .
Композиционные функции называют сложными, и этот термин многим из вас хорошо знаком. Образно говоря, в композициях одна функция вложена в
другую.
 1.2. Основы математической логики 1.2. Основы математической логики
 1.1.6. Обратное отображение 1.1.6. Обратное отображение
| Оглавление |
|

 Высшая алгебра для начинающих
Высшая алгебра для начинающих 1.2. Основы математической логики
1.2. Основы математической логики 1.1.6. Обратное отображение
1.1.6. Обратное отображение